Proposizione 8   Sia $G = < a >$ un gruppo ciclico, e sia

\begin{displaymath}\mathcal{H} := \{H\mid H\;\mbox{ sottogruppo}\; di\; G \}.\end{displaymath}

Se $\vert G\vert$ è infinito i sottogruppi di $G$ diversi da $\{1\}$, hanno ordine infinito, ed esiste una corrispondenza biunivoca

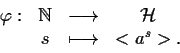
\begin{displaymath}\begin{array}{cccc} \varphi: & \mathbb{N} &\longrightarrow &\mathcal{H}\\ & s &\longmapsto &< a^{s} >.\end{array}\end{displaymath}

Se $G$ è finito di ordine $t$, esiste una corrispondenza biunivoca

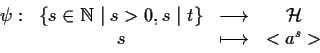
\begin{displaymath}\begin{array}{cccc} \psi: & \{s\in \mathbb{N}\mid s > 0 , s\m... ...ow &\mathcal{H}\\ & s & \longmapsto &< a^{s} > \end{array}\end{displaymath}

con $\mid < a^{s} >\mid = t/s$ . In particolare, l'ordine di ogni sottogruppo è un divisore di $t$, e per ogni divisore positivo $q$ di $t$ esiste uno ed un solo sottogruppo di ordine $q$, cioè $<a^{t/q}>.$

Dimostrazione
Supponiamo che $\vert G\vert$ sia infinito.
Per proposizione 7 della sezione "Gruppi e sottogruppi ciclici", $\forall s\in \mathbb{N}\setminus \{0\}$, gli elementi $a^{ms}$, al variare di $m$ in $\mathbb{Z} $, sono distinti e quindi $\vert H\vert = \vert< a^{s} >\vert$ è infinito $\forall s$.
Inoltre l'applicazione $\varphi$ è suriettiva per proposizione 2 della sezione "Gruppi e sottogruppi ciclici", e ogni sottogruppo $H$ è della forma $< a^{s} >$, dove $s$ è il più piccolo intero positivo tale che $a^{s} \in H$. Essendo $\vert G\vert$ infinito $a^{s}$ è l'unico generatore per $H$ con esponente positivo; infatti se $<a^{t}>=<a^{s}>$ con $t>0$, $s>0$, si ha $a^{t}=(a^{s})^{q}$ e $a^{s}=(a^{t})^{l}$ da cui per proposizione 7 della sezione "Gruppi e sottogruppi ciclici", $t=sq$ e $s=tl$, cioè $\vert s\vert\leq \vert t\vert$ e $\vert t\vert \leq \vert s\vert$, da cui $s=t$. Allora se $\varphi (s) = \varphi (t) $, cioè $< a^{s}> = <a^{t}>$, per la minimalità di $s$ e $t$, si ha $s=t$.
Supponiamo ora che $G$ abbia ordine finito $t$: $G = \{1,... ,a^{t-1}\}$.
Se $H = < 1 >$, $H = < a^{t} >$, $t\mid t$ e $\vert<1>\vert=t/t$.
Se $H \ne < 1 >$, sia $s$ il più piccolo intero positivo tale che $a^{s} \in H$; da proposizione 2 segue $H = < a^{s} >$.
Proviamo che $s\mid t$. Dividiamo $t$ per $s$:

\begin{displaymath}t = s q + r \qquad \mbox{ con} \quad 0\leq r < s.\end{displaymath}

Si ha allora: $1 = a^{t} = a^{s q + r } = a^{sq} a^{r} \;$ cioè $\; a^{r} = (a^{s})^{-q} \in H$. Quindi $r =0$, per la minimalità di $s$, e $t=sq$, cioè $s\mid t$.
Proviamo ora che $q$ è l'ordine di $< a^{s} >$: $q>0$, $(a^{s})^{q} = a^{t} = 1$, e se esistesse $0<q' < q$ tale che $(a^{s})^{q'} = 1$, si avrebbe $sq'>0$, $a^{sq'}=0$, e $sq'<t$, che è assurdo essendo $\left\vert a \right\vert = t$.
Consideriamo ora l'applicazione $\psi:$ $\psi$ è suriettiva per quanto appena visto. Inoltre, $\psi$ è iniettiva in quanto se $\psi (s) = \psi (l)$, cioè $< a^{s} > = < a^{l} > $, i due sottogruppi hanno lo stesso ordine, cioè $t/s =t/l$, da cui $s=l$.

Corollario 9   Sia $G$ un gruppo ciclico di ordine $t$ e sia $q\in\mathbb{N} $ tale che $q\mid t$. Allora il sottogruppo $H$ di ordine $q$ di $G$ è l'insieme degli elementi $b$ di $G$ tali che $b^{q} = 1$.

Dimostrazione
Sia $G = < a >$.
Dalla proposizione 8 segue che se $H$ è il sottogruppo di $G$ di ordine $q$, $H = < a^{t/q}>$.
Allora se $b\in H$, $b = (a^{t/q})^{k}$, con $k\in \mathbb{Z} $ e $b^{q} = (a^{k\cdot t/q})^{q} = (a^{t})^{k} = 1$.
Se viceversa $b\in G$ è tale che $b^{q} = 1$ si ha $b = a^{k}$ e $(a^{k})^{q} = 1$. Poiché $\left\vert a \right\vert = \left\vert G \right\vert = t $, per proposizione 6 $t \vert kq$ e quindi $kq = tm$, con $m\in \mathbb{Z} $, cioè $k = mt/q$; allora $b = a^{k} = (a^{t/q})^{m} \in H$.


previousup next esercizi