Proposizione 2
Se
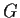
è un gruppo ciclico, si ha :
- 1)
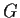 è abeliano;
è abeliano;
- 2)
- se
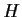 è un sottogruppo di
è un sottogruppo di 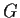 ,
allora
,
allora 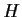 è ciclico, e
se
è ciclico, e
se
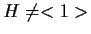 ,
allora
,
allora 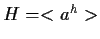 dove
dove 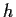 è il più piccolo intero positivo tale che
è il più piccolo intero positivo tale che
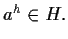
Dimostrazione
- 1)
- Se
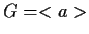 e
e 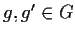 ,
si ha
,
si ha 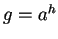 e
e
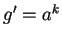 con
con
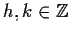 .
.
Allora
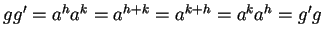 .
.
- 2)
- Sia
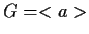 .
.
Se 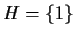 ,
allora
,
allora
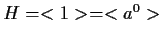 .
.
Se
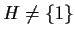 ,
sia
,
sia 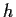 il più piccolo intero (strettamente)
positivo tale che
il più piccolo intero (strettamente)
positivo tale che
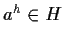 .
Tale intero esiste, infatti
essendo
.
Tale intero esiste, infatti
essendo
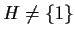 ,
esiste un intero non nullo
,
esiste un intero non nullo 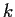 tale che
tale che
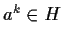 ;
se
;
se 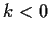 ,
,
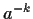 è l'inverso di
è l'inverso di 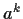 e quindi appartiene
ad
e quindi appartiene
ad 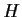 .
Allora l'insieme
.
Allora l'insieme
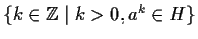 è non vuoto e quindi ammette minimo.
è non vuoto e quindi ammette minimo.
Sia allora 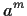 un elemento di
un elemento di 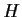 .
Dividiamo
.
Dividiamo 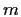 per
per 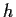 :
:
Consideriamo:
poiché 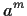 e
e
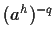 appartengono entrambi ad
appartengono entrambi ad 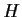 .
.
Allora 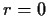 per la minimalità di
per la minimalità di 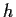 ,
e quindi
,
e quindi 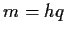 .
.
Si ha dunque:
cioè
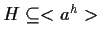 .
Poiché ovviamente
.
Poiché ovviamente
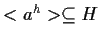 ,
possiamo concludere
che
,
possiamo concludere
che
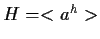 .
.