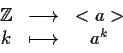Definizione 4
Sia 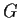 un gruppo. L'ordine di
un gruppo. L'ordine di 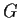 è la cardinalità
di
è la cardinalità
di 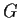 e si indica con
e si indica con
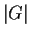 .
.
Definizione 5
Sia ![]() un gruppo e sia
un gruppo e sia ![]() .
.
Se
![]() ,
,
![]() ,
si dice che
,
si dice che ![]() ha periodo o
ordine infinito; se invece
ha periodo o
ordine infinito; se invece
![]() tale che
tale che ![]() si dice che
si dice che ![]() ha
periodo o ordine
ha
periodo o ordine ![]() ,
dove
,
dove ![]() è il più piccolo intero
positivo tale che
è il più piccolo intero
positivo tale che ![]() .
.
L'ordine di ![]() viene denotato
con
viene denotato
con
![]() .
.
 |
Gruppo ciclico infinito generato dall'elemento a. |
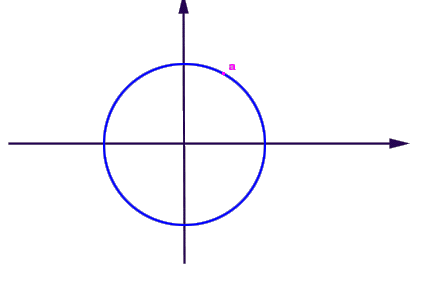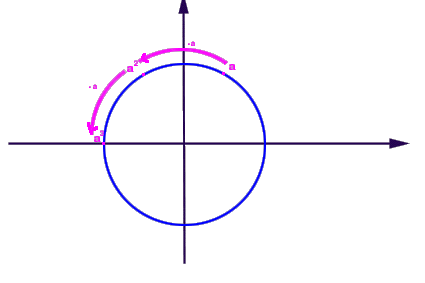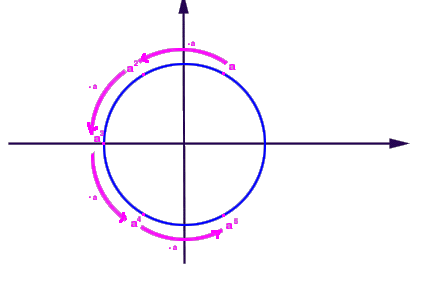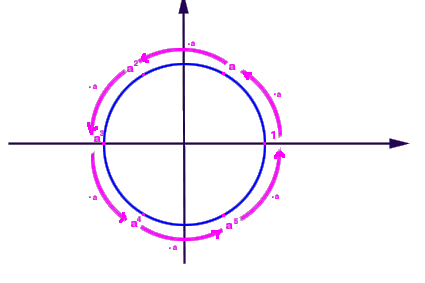 |
Gruppo ciclico di ordine 6 generato dall'elemento a. |
Proposizione 6
Sia ![]() un gruppo e sia
un gruppo e sia ![]() .
.
Se ![]() ha ordine finito
ha ordine finito ![]() ,
allora un intero
,
allora un intero ![]() è tale che
è tale che ![]() se e solo se
se e solo se ![]() .
.
Dimostrazione
Sia ![]() .
.
Dividiamo ![]() per
per ![]() :
:
Allora
quindi
Sia ora
Si ha allora: