Esempio 8
L'insieme
dove
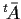
è la trasposta della
matrice coniugata di
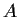
(ricordiamo che se
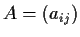
,
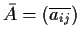
), è un sottogruppo di
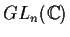
,
chiamato
gruppo unitario di ordine
n.
Infatti
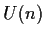
è un sottoinsieme di
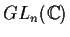
in quanto
cioè
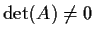
.
Moltiplicando entrambi i membri dell'uguaglianza
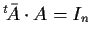
a sinistra per
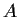
,
si ottiene
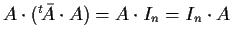
,
cioè
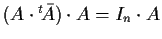
da cui per cancellazione
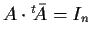
e dunque
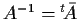
.
Inoltre:
-
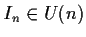 ;
;
- se
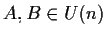 ,
,
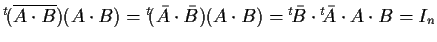 ,
cioè
,
cioè
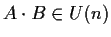 ;
;
- se
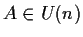 ,
,
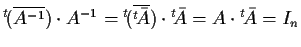 .
Allora
.
Allora
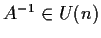 .
.
Inoltre, poiché
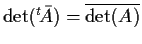
,
si
ha
quindi
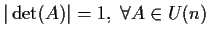
.
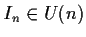 ;
;
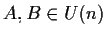 ,
,
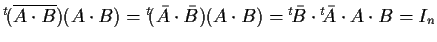 ,
cioè
,
cioè
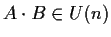 ;
;
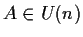 ,
,
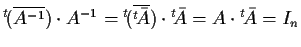 .
Allora
.
Allora
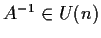 .
.