24 ESEMPIO
Due sottospazi proiettivi
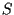
ed
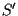
di
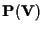
aventi la stessa dimensione sono proiettivamente equivalenti.
Infatti, se
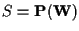
ed
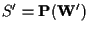
con
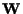
e
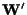
sottospazi vettoriali di
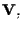
esiste
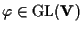
tale che
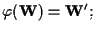
pertanto, se
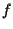
è la proiettività indotta da
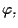
allora
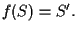
26 OSSERVAZIONE
Dal
teorema 17 segue che due sottoinsiemi di
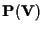
costituiti ognuno da
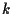
punti in posizione generale sono proiettivamente equivalenti se
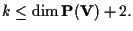
Se invece
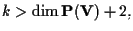
ciò non è vero già nel caso di
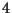
punti di una retta proiettiva.

