20 DEFINIZIONE
Siano
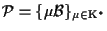
e
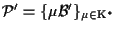
due riferimenti proiettivi su
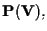
dove
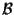
e
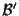
sono basi di
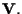
Allora le equazioni dell'identità su
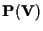
rispetto ai riferimenti proiettivi
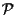
e
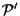
sono dette
equazioni del cambiamento di coordinate
omogenee da
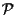
a
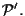
21 OSSERVAZIONE
Siano
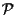
e
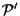
come nella definizione precedente. Sia
![$P=[x_0,\ldots,x_n]_{\mathcal{P}}.$](img11.gif)
Allora esistono coordinate omogenee
![$[y_0,\ldots,y_n]$](img12.gif)
per
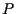
tali che
![$P=[y_0,\ldots,y_n]_{\mathcal{P'}}$](img14.gif)
e
Viceversa: se
![$P=[a_0,\ldots,a_n]_{\mathcal{P}}= [b_0,\ldots,b_n]_{\mathcal{P'}},$](img16.gif) allora esiste
allora esiste
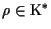 tale che
tale che
22 OSSERVAZIONE
Siano
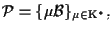
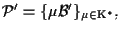
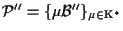
tre riferimenti proiettivi su
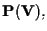
dove
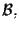
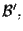
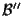
sono basi di
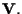
Allora le equazioni del cambiamento di coordinate omogenee da
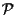
a
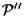
sono date dalla matrice
mentre il cambiamento di coordinate omogenee da
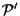 a
a
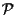 è espresso dalla matrice
è espresso dalla matrice
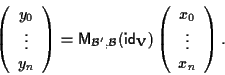
![]() allora esiste
allora esiste
![]() tale che
tale che
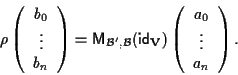
![]() a
a
![]() è espresso dalla matrice
è espresso dalla matrice



