Infatti le due terne di punti sono in posizione generale, quindi (proposizione 17) esiste un'unica
Allora
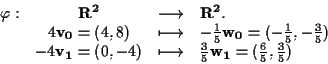
Siano
Le equazioni di
Invece le equazioni di
cioè dalla matrice
che è esattamente
Quindi equazioni di ![]() rispetto ad
rispetto ad
![]() sono
sono
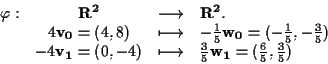
cioè dalla matrice
che è esattamente
Quindi equazioni di ![]() rispetto ad
rispetto ad
![]() sono
sono

|
 |
 |