Consideriamo in
Per ogni
chiamata proiezione stereografica di
![]() su
su ![]()
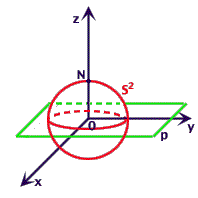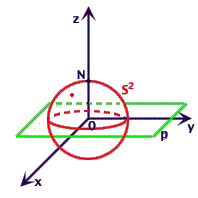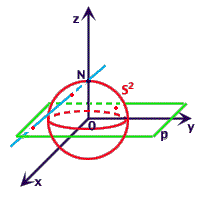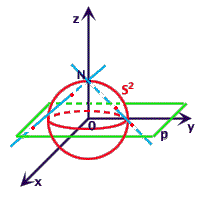
Sia
Poiché la retta
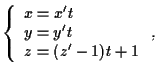 intersecando con
intersecando con Viceversa: dato
Quindi
Analiticamente poi si vede che
![]() L'applicazione
L'applicazione ![]() consente quindi di rappresentare la sfera
consente quindi di rappresentare la sfera
![]() come il piano
come il piano ![]() a cui è stato aggiunto il punto
a cui è stato aggiunto il punto ![]() Inoltre, se identifichiamo
Inoltre, se identifichiamo ![]() con
con
![]() con l'applicazione
con l'applicazione
e ricordiamo che
![]() è identificabile a
è identificabile a
![]() (esempio 5 della sezione "Completamento di uno spazio affine"), otteniamo un'applicazione biunivoca
(esempio 5 della sezione "Completamento di uno spazio affine"), otteniamo un'applicazione biunivoca
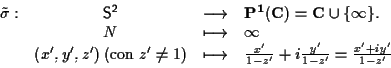
In effetti il punto ![]() può essere interpretato come "punto all'infinito" di
può essere interpretato come "punto all'infinito" di ![]() poiché all'allontanarsi di
poiché all'allontanarsi di ![]() dall'origine
dall'origine ![]() cioè al tendere di
cioè al tendere di
![]() all'infinito,
all'infinito,
![]() si avvicina ad
si avvicina ad ![]()
La sfera fornisce in questo modo un modello geometrico di
![]() chiamato sfera di Riemann.
chiamato sfera di Riemann.



