3 OSSERVAZIONE
L'applicazione
è iniettiva, e risulta, identificando
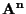 con
con
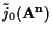 e
e 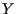 con
con
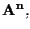
Per ottenere
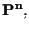
abbiamo cioè aggiunto ad
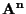
l'insieme
delle rette per l'origine; in altre parole,
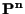
si ottiene
aggiungendo ad
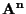
le direzioni delle sue rette.
5 ESEMPIO
In
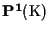
sarà
![$H_0=\{ [0,1]\};$](img19.gif)
tale punto viene spesso
denotato col simbolo
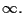
Se si identifica
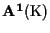
con
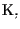
risulterà
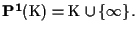
Pertanto talvolta si
usa una sola coordinata non omogenea su
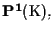
tenendo
conto dell'inclusione.
![]() con
con
![]() e
e ![]() con
con
![]()
![]() con
con
![]() e
e ![]() con
con
![]()



