1 OSSERVAZIONE
È facile generalizzare gli
esempi 8 e
9 della sezione "Definizione di spazio
proiettivo". Consideriamo
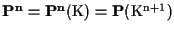
come
l'insieme delle rette affini di
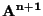
passanti per l'origine: ogni
punto
![$[x_0,x_1,\ldots,x_n] \in \mathbf{P^n}$](img3.gif)
corrisponde alla retta di
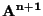
costituita dai punti
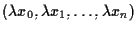
al variare di
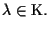
I punti
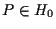
corrispondono alle rette contenute nell'iperpiano affine di
equazione
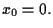
Chiamiamo tale iperpiano
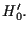
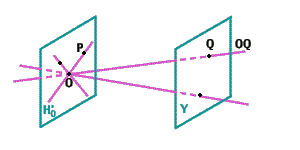
Consideriamo l'iperpiano affine
di
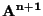
di equazione
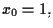
cioè
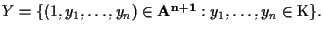
Ogni punto
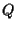
di
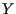
corrisponde ad una retta affine di
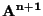
passante per
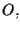
che chiamiamo
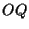
tale retta non è parallela ad
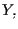
quindi
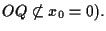
Infatti se
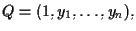
allora sarà
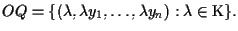
Viceversa, ogni retta
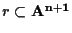
passante per
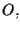
ad
eccezione delle rette parallele ad
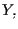
corrisponde a un punto di
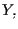
che è il
punto
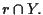
Le rette parallele ad
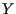
passanti per
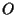
sono le rette contenute
nell'iperpiano
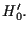
Si ottiene cosí una corrispondenza biunivoca
con inversa:
L'applicazione
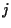
induce pertanto una corrispondenza biunivoca tra
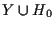
e
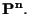
Si noti inoltre che i punti di
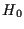
sono le rette vettoriali di
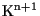
contenute nella giacitura di
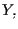
che è appunto l'iperpiano
vettoriale
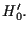
In poche parole:
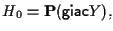
e si ha quindi
una biezione naturale
Si osservi che
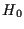
ed
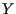
possono essere sostituiti da un qualsiasi iperpiano
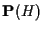
di
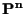
e da un iperpiano affine di
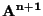
avente giacitura
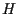
e non passante per l'origine.
Se nella costruzione precedente identifichiamo
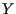
con
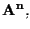
utilizzando l'applicazione biunivoca
componendo
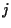
con
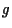
otteniamo l'applicazione biunivoca
la cui inversa è




