Consideriamo
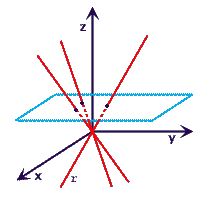

Essendo poi il piano
![]() in corrispondenza biunivoca con il piano
affine reale
in corrispondenza biunivoca con il piano
affine reale
![]() ,
possiamo dire che l'insieme dei punti di
,
possiamo dire che l'insieme dei punti di
![]() è in corrispondenza biunivoca con l'insieme dei punti di
è in corrispondenza biunivoca con l'insieme dei punti di
![]() e delle direzioni
delle
rette di
e delle direzioni
delle
rette di
![]()
In questo modo abbiamo "allargato"
![]() per
evitare alcune eccezioni (per esempio: due rette in un
piano affine si incontrano in un punto o sono
parallele), chiamando "punti" tutti i punti di
per
evitare alcune eccezioni (per esempio: due rette in un
piano affine si incontrano in un punto o sono
parallele), chiamando "punti" tutti i punti di
![]() e anche tutte le direzioni delle rette
di
e anche tutte le direzioni delle rette
di
![]() .
.



