chiusura proiettiva di un sottospazio affine

8 PROPOSIZIONE-DEFINIZIONE Siano $y_1,\ldots,y_n$ le coordinate di un punto variabile in $\mathbf{A^n}=\mathbf{A^n}(\mathrm{K}),$ e siano $x_0,\ldots,x_n$ le coordinate omogenee di un punto variabile in $\mathbf{P^n}=\mathbf{P^n}(\mathrm{K}).$ Si consideri un iperpiano

di $\mathbf{A^n},$ di equazione $a_1Y_1+\cdots+a_nY_n+a_0=0 \; \; (\ast).$
Allora l'applicazione $j_0:\mathbf{A^n} \longrightarrow \mathbf{P^n} \setminus H_0$ definita nell'osservazione 1 trasforma i punti di

nei punti propri

rispetto a

dell'iperpiano

di $\mathbf{P^n}$ di equazione $a_0X_0+a_1X_1+\cdots+a_nX_n=0 \; \; (\ast \ast).$
L'iperpiano

è detto chiusura proiettiva di

Dimostrazione
Se $(y_1,\ldots,y_n)$ soddisfa $(\ast),$ allora $j_0(y_1,\ldots,y_n)=[1,y_1,\ldots,y_n]$ soddisfa $(\ast \ast).$
Viceversa, se $[x_0,x_1,\ldots,x_n] \in H$ è un punto proprio

rispetto a

allora $x_0 \neq 0$ e $j_0^{-1}[x_0,x_1,\ldots,x_n]=(\frac{x_1}{x_0},\ldots, \frac{x_n}{x_0})$ soddisfa $(\ast).$

10 PROPOSIZIONE-DEFINIZIONE Piú in generale, si consideri un sottospazio affine

di $\mathbf{A^n}=\mathbf{A^n}(\mathrm{K}),$ definito dal sistema di equazioni lineari

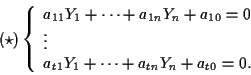
$\begin{displaymath}(\star) \left\{ \begin{array}{l} a_{11}Y_1+\cdots+a_{1n}Y_n+... ...ts \\ a_{t1}Y_1+\cdots+a_{tn}Y_n+a_{t0}=0. \end{array} \right.\end{displaymath}$

Allora l'applicazione trasforma i punti di nei punti propri rispetto a del sottospazio di $\mathbf{P^n}=\mathbf{P^n}(\mathrm{K})$ di equazioni cartesiane

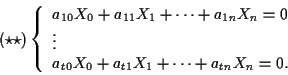
$\begin{displaymath}(\star \star) \left\{ \begin{array}{l} a_{10}X_0+a_{11}X_1+\... ...\\ a_{t0}X_0+a_{t1}X_1+\cdots+a_{tn}X_n=0. \end{array} \right.\end{displaymath}$

Il sottospazio è detto chiusura proiettiva di

Dimostrazione
È analoga alla dimostrazione della proposizione 8: basta sostituire

con

e $(\ast),$ $(\ast \ast)$ con $(\star),$ $(\star \star).$