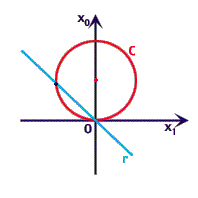
5 OSSERVAZIONE   Un altro modo di descrivere $\mathbf{P^1(R)}$ si ottiene considerando la circonferenza $\mathsf{C} \subset \mathsf{E^2}$ di raggio $1$ e centro nel punto $(0,1).$

Le rette per l'origine diverse dall'asse $x_0=0$ $($cioè quelle che rappresentano i punti di $\mathbf{P^1(R)} \setminus H_0)$ incontrano $\mathsf{C}$ in due punti, di cui uno è $(0,0)$ e l'altro è variabile; invece la retta $x_0=0$ incontra $\mathsf{C}$ solo in $(0,0).$
Facendo corrispondere alla retta vettoriale $r \subset \mathsf{E^2}$ variabile la sua intersezione $\gamma (r)$ con $\mathsf{C}$ diversa da $(0,0),$ si definisce una corrispondenza biunivoca

\begin{displaymath}\begin{array}{cccl} \gamma: & \mathbf{P^1(R)} \setminus H_0 ... ...gmapsto & (r \cap \mathsf{C}) \setminus \{ (0,0) \} \end{array}\end{displaymath}

Ponendo $\gamma (H_0)=(0,0),$ $\gamma$ si estende a una corrispondenza biunivoca

\begin{displaymath}\tilde{\gamma}:\mathbf{P^1(R)} \longrightarrow \mathsf{C}.\end{displaymath}

In questo modo si ottiene una circonferenza come modello geometrico di $\mathbf{P^1(R)}.$

PAGINA PRECEDENTE INIZIO PAGINA PAGINA SUCCESSIVA PERCORSO SUGGERITO