17 ESERCIZIO   Determinare un'equazione cartesiana del piano di $\mathbf{P^3(R)}$ passante per il punto $[1,1,0,1]$ e per i punti impropri rispetto a $j_0$ delle rette $r'$ ed $s'$ di $\mathbf{A^3(R)}$ di equazioni :


\begin{displaymath}r':\left\{ \begin{array}{l} X+Y+Z-1=0 \\ 2X-Y-Z=0 \end{array... ...{ \begin{array}{l} 2X-Y-2Z+1=0 \\ Y+Z-1=0. \end{array} \right.\end{displaymath}

VAI ALLA SOLUZIONE
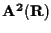
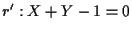
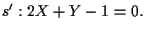
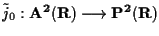
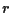
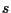
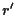
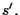
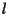
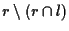
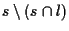
18 ESERCIZIO   In $\mathbf{A^2(R)}$ consideriamo le rette $r':X+Y-1=0$ ed $s':2X+Y-1=0.$ Consideriamo il completamento proiettivo $\tilde{j}_0 :\mathbf{A^2(R)} \longrightarrow \mathbf{P^2(R)}$ del piano affine reale, e siano $r$ ed $s$ le chiusure proiettive di $r'$ ed $s'.$ Si determini l'equazione di una retta $l$ tale che le rette affini di $r \setminus (r \cap l)$ ed $s \setminus (s \cap l)$ nel piano affine avente $l$ 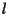come retta impropria $($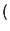cioè: come retta che, unita ad $\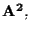mathbf{A^2},$ dà $\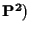mathbf{P^2})$ sono parallele.

Suggerimento   
VAI ALLA SOLUZIONE