Soluzione
Le chiusure proiettive di $r'$ ed $s'$ sono le rette $r,s \subset \mathbf{P^3(R)}$ di equazioni cartesiane:


\begin{displaymath}r:\left\{ \begin{array}{l} -X_0+X_1+X_2+X_3=0 \\ 2X_1-X_2-X_... ...{l} X_0+2X_1-X_2-2X_3=0 \\ -X_0+X_2+X_3=0. \end{array} \right.\end{displaymath}

I loro punti impropri rispetto a $j_0$ sono dati dall'intersezione con l'iperpiano $H_0$ di equazione $X_0=0,$ quindi sono le soluzioni dei sistemi seguenti:


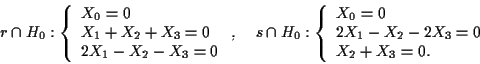
\begin{displaymath}r \cap H_0 :\left\{ \begin{array}{l} X_0=0 \\ X_1+X_2+X_3=0 ... ...l} X_0=0 \\ 2X_1-X_2-2X_3=0 \\ X_2+X_3=0. \end{array} \right.\end{displaymath}

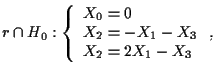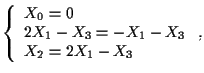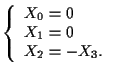
Pertanto $r \cap H_0 :\left\{ \begin{array}{l} X_0=0 \\ X_2=-X_1-X_3 \\ X_2=2X_1-X_3 \end{array} \right.,$ cioè $\left\{ \begin{array}{l} X_0=0 \\ 2X_1-X_3=-X_1-X_3 \\ X_2=2X_1-X_3 \end{array} \right.,$ ovvero $\left\{ \begin{array}{l} X_0=0 \\ X_1=0 \\ X_2=-X_3. \end{array} \right.$
Quindi $r \cap H_0=[0,0,1,-1].$
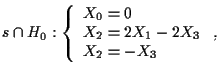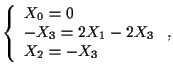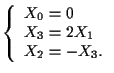
Analogamente $s \cap H_0 :\left\{ \begin{array}{l} X_0=0 \\ X_2=2X_1-2X_3 \\ X_2=-X_3 \end{array} \right.,$ cioè $\left\{ \begin{array}{l} X_0=0 \\ -X_3=2X_1-2X_3 \\ X_2=-X_3 \end{array} \right.,$ ovvero $\left\{ \begin{array}{l} X_0=0 \\ X_3=2X_1 \\ X_2=-X_3. \end{array} \right.$
Quindi $s \cap H_0=[0,1,-2,2].$
Un'equazione cartesiana del piano passante per i punti $[1,1,0,1],$ $[0,0,1,-1]$ e $[0,1,-2,2]$ è dunque data da (vedi l'esempio 13 della sezione "Equazioni di un sottospazio proiettivo")


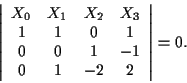
\begin{displaymath}\left\vert \begin{array}{cccc} X_0 & X_1 & X_2 & X_3 \\ 1 &... ... 0 & 0 & 1 & -1 \\ 0 & 1 & -2 & 2 \end{array} \right\vert =0.\end{displaymath}

Sviluppando tale determinante rispetto alla terza riga, otteniamo quindi


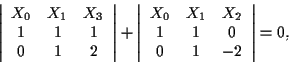
\begin{displaymath}\left\vert \begin{array}{ccc} X_0 & X_1 & X_3 \\ 1 & 1 & 1 ... ...& X_2 \\ 1 & 1 & 0 \\ 0 & 1 & -2 \end{array} \right\vert =0,\end{displaymath}

cioè $X_0-2X_1+X_3-2X_0+2X_1+X_2=0,$ ovvero $-X_0+X_2+X_3=0.$
TORNA ALLA TEORIA