Soluzione
Le chiusure proiettive di 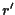 ed
ed 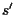 sono
sono
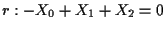 ed
ed
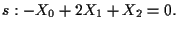
Il loro punto di intersezione è
![$P=r \cap s=\{ [X_0,X_1,X_2] \in
\mathbf{P^2(R)}:
(\ast) \left\{ \begin{array}{l}
-X_0+X_1+X_2=0 \\
-X_0+2X_1+X_2=0
\end{array} \right. \}.$](img22.gif)
Il sistema 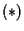 equivale al sistema
equivale al sistema
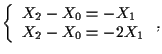 cioè a
cioè a
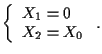 Quindi
Quindi
![$P=r \cap s=[1,0,1].$](img26.gif)
Si può scegliere allora come retta 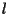 distinta da
distinta da 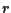 ed
ed 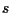 la retta di
equazione
la retta di
equazione 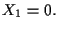
Nel piano affine
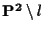 che ha tale retta come retta
impropria, le equazioni di
che ha tale retta come retta
impropria, le equazioni di 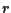 ed
ed 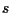 sono
sono 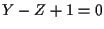 e
e 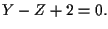

![$P=r \cap s=\{ [X_0,X_1,X_2] \in
\mathbf{P^2(R)}:
(\ast) \left\{ \begin{array}{l}
-X_0+X_1+X_2=0 \\
-X_0+2X_1+X_2=0
\end{array} \right. \}.$](img22.gif)
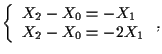 cioè a
cioè a
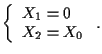 Quindi
Quindi
