

10 ESERCIZIO
Verificare se le rette di
![]()
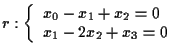 e
e
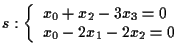
sono sghembe oppure incidenti.

11 ESERCIZIO
Siano
![]() ed
ed
![]() campi, con
campi, con
![]() Dimostrare che ogni iperpiano di
Dimostrare che ogni iperpiano di
![]() ha almeno un punto
appartenente a
ha almeno un punto
appartenente a
![]() se e solo se la dimensione di
se e solo se la dimensione di
![]() considerato come spazio vettoriale su
considerato come spazio vettoriale su
![]() è minore o
uguale di
è minore o
uguale di ![]()
