Soluzione
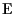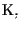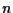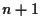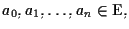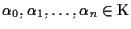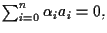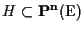La dimensione di $\mathrm{E}$ come spazio vettoriale su $\mathrm{K},$ è minore o uguale di $n$ se e solo se, dati $n+1$ vettori qualsiasi $a_0,a_1,\ldots,a_n \in \mathrm{E},$ esistono $\alpha_0,\alpha_1,\ldots,\alpha_n \in \mathrm{K}$ non tutti nulli tali che $\sum_{i=0}^n \alpha_i a_i =0,$ cioè se e solo se per ogni iperpiano $H \subset \mathbf{P^n}(\mathrm{E})$ di equazione 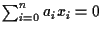$\sum_{i=0}^n a_i x_i =0$ esistono 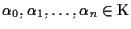$\alpha_0,\alpha_1,\ldots,\alpha_n \in \mathrm{K}$ non tutti nulli tali che $\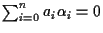sum_{i=0}^n a_i \alpha_i=0$ e quindi se e solo se per ogni iperpiano $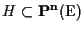H \subset \mathbf{P^n}(\mathrm{E})$ esiste almeno un punto $[\alpha_0,\alpha_1,\ldots,\alpha_n] \in \mathbf{P^n}(\mathrm{K})$ appartenente ad $H.$
TORNA ALLA TEORIA