PUNTI FONDAMENTALI E PUNTO UNITA'

10 PROPOSIZIONE Siano $\mathcal{B}=(\mathbf{v}_0,\ldots,\mathbf{v}_n),\; \mathcal{B'}=(\mathbf{w}_0,\ldots,\mathbf{w}_n)$ basi di $\mathbf{V}.$
Allora $[\mathbf{v_0} ] = [\mathbf{w_0} ], \ldots, [\mathbf{v_n} ] = [\mathbf{w_n} ], [\mathbf{v_0 + \cdots + v_n} ] = [\mathbf{w_0 + \cdots + w_n} ]$ se e solo se esiste $\lambda \in \mathrm{K}^{\ast}$ tale che $\mathbf{v_i} = \lambda \mathbf{w_i}$ per ogni $i = 0, \ldots, n$

cioè se e solo se esiste $\lambda \in \mathrm{K}^{\ast}$ tale che $\mathcal{B}= \lambda \mathcal{B'}).$

Dimostrazione
$\Leftarrow \;)$ ovvia
$\Rightarrow \;)$ Supponiamo che $[\mathbf{v_i} ] = [\mathbf{w_i} ]$ per $i = 0, \ldots, n$ e $[\mathbf{v_0 + \cdots + v_n} ] = [\mathbf{w_0 + \cdots + w_n} ],$ allora esistono $\lambda_0, \ldots, \lambda_n, \lambda_{n + 1} \in \mathrm{K}^{\ast}$ tali che $\mathbf{v_0} = \lambda_0 \mathbf{w_0}, \ldots, \mathbf{v_n} = \lambda_n \mathbf... ...\; \mathbf{v_0 + \cdots + v_n} = \lambda_{n + 1} (\mathbf{w_0 + \cdots + w_n}),$ quindi $\lambda_0 \mathbf{w_0} + \cdots + \lambda_n \mathbf{w_n} = \lambda_{n + 1} \mathbf{w_0} + \cdots + \lambda_{n + 1} \mathbf{w_n}.$
Ma $\mathcal{B'}$ è una base di $\mathbf{V},$ pertanto i vettori di $\mathbf{V}$ sono scritti in modo unico come combinazione lineare degli elementi di tale base. Quindi i coefficienti a sinistra dell'uguaglianza precedente devono essere uguali a quelli di destra, cioè $\lambda_0 = \lambda_{n + 1}, \ldots, \lambda_n = \lambda_{n + 1}.$ Quindi, prendendo $\lambda = \lambda_{n + 1},$ segue $\mathcal{B}= \lambda \mathcal{B'}.$

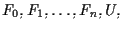
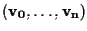
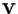
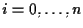
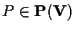
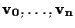
11 OSSERVAZIONE Una (n+2)-pla di punti $F_0, F_1, \ldots, F_n, U,$ tale che esiste una base $(\mathbf{v_0}, \ldots,\mathbf{v_n} )$ di $\mathbf{V}$ tale che $F_i = [\mathbf{v_i} ]$ per $i = 0, \ldots, n$ e $U = [\mathbf{v_0 + \cdots + v_n} ],$ è sufficiente per associare coordinate omogenee ad ogni punto $P \in \mathbf{P(V)}$ nel modo seguente: i vettori $\mathbf{v_0}, \ldots, \mathbf{v_n}$ determinano, come visto nella proposizione 10, una base per $\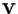mathbf{V}$ ben definita a meno di un fattore di proporzionalità non nullo, quindi determinano un riferimento proiettivo. Al punto

assegneremo le coordinate secondo questo riferimento.
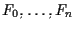
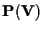
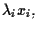
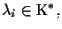
Invece n+1 punti $F_0, \ldots, F_n$ linearmente indipendenti in $\mathbf{P(V)}$ non sono sufficienti per determinare le coordinate omogenee di un punto (come visto nell'esempio 6), poiché gli $F_i = [\mathbf{v_i} ]$ potrebbero essere rappresentati da $\lambda_i x_i,$ per arbitrari $\lambda_i \in \mathrm{K}^{\ast},$ non necessariamente uguali per ogni

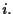
L'ambiguità viene quindi risolta solo aggiungendo un (n+2)-esimo punto.

12 OSSERVAZIONE Si può notare che, mentre per uno spazio vettoriale n-dimensionale un sistema di coordinate richiede n punti (una base) e per uno spazio affine n-dimensionale n+1 punti (un riferimento affine), per uno spazio proiettivo ne richiede addirittura n+2.

13 DEFINIZIONE Dato un riferimento proiettivo $\mathcal{P} = \{ \mu \mathcal{B} \}_{\mu \in \mathrm{K}^{\ast}},$ dove $\mathcal{B} = (\mathbf{v}_0, \ldots, \mathbf{v}_n)$ è una base di $\mathbf{V},$ i punti $[\mathbf{v_0} ], \ldots, [\mathbf{v_n} ]$ sono detti punti fondamentali di $\mathcal{P},$ il punto $U = [\mathbf{v_0 + \cdots + v_n} ]$ è detto punto unità di $\mathcal{P}.$

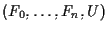
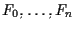
14 OSSERVAZIONE Data una (n+2)-pla di punti $(F_0, \ldots, F_n, U)$ come nell'osservazione 11, $F_0, \ldots, F_n$ sono i punti fondamentali e

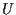
è il punto unità.

15 ESEMPIO