6 ESEMPIO
Consideriamo la base
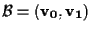
di
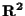
e modifichiamola moltiplicando ciascun vettore per
scalari diversi, per esempio prendendo la base
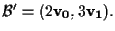
Allora le coordinate proiettive
cambiano (da notare che, al contrario, come visto nella
proposizione 3, se modifichiamo
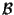
moltiplicando tutti i
vettori per lo stesso scalare
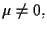
le coordinate proiettive
non cambiano).
Infatti sia
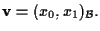
Allora
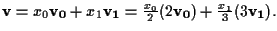
Quindi
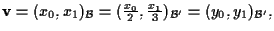
dove
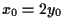
e
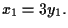
Sia
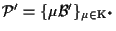
il riferimento proiettivo associato a
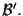
Allora


