coordinate omogenee

1 CONVENZIONE Se $\mathcal{B} = (\mathbf{v_1}, \ldots,\mathbf{v_n})$ è una base di $\mathbf{V},$ e $\mathbf{v} = \lambda_1 \mathbf{v_1} + \cdots + \lambda_n \mathbf{v_n} \in \mathbf{V},$ scriviamo $\mathbf{v} = (\lambda_1, \ldots,\lambda_n)_{\mathcal{B}}.$
Nel caso di $\mathrm{K}^n$ ed $\mathcal{E}$ (base canonica di $\mathrm{K}^n$ ), si scrive solo $(\lambda_1, \ldots,\lambda_n).$
La base canonica di $\mathrm{K}^{n+1},$ d'ora in poi, è denotata con $\mathcal{E} = (\mathbf{e_0}, \ldots, \mathbf{e_n}).$

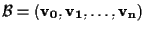
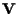
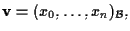
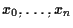
2 DEFINIZIONE Vogliamo ora dare coordinate ai punti di uno spazio proiettivo. 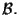Data $\mathcal{B}=(\mathbf{v_0}, \mathbf{v_1},\ldots,\mathbf{v_n})$ base di $\mathbf{V}$ , possiamo associare a un punto $[\mathbf{v}] \in \mathbf{P(V)}$ una (n+1)-pla di coordinate in questo modo: se $\mathbf{v} = (x_0, \ldots,x_n)_{\mathcal{B}},$ allora diciamo che $x_0, \ldots,x_n$ sono le coordinate omogenee del punto $[\mathbf{v}]$ rispetto a $\mathcal{B}.$
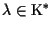
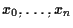
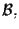
Tali coordinate sono determinate a meno di un fattore di proporzionalità non nullo. 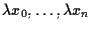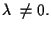Infatti, dato $\lambda \in \mathrm{K}^{\ast}$ , vale $[\mathbf{v} ]=[\lambda \mathbf{v} ]$ , e $\lambda \mathbf{v} = \lambda x_0 \mathbf{v_0} + \lambda x_1 \mathbf{v_1} + \cdots + \lambda x_n \mathbf{v_n}.$ Quindi, se $x_0, \ldots,x_n$ sono coordinate omogenee di $[\mathbf{v}]$ rispetto a $\mathcal{B},$ lo sono anche $\lambda x_0, \ldots , \lambda x_n$ per ogni $\lambda \; \neq 0.$

Dimostrazione
Sia $\mathcal{B}=(\mathbf{v_0}, \mathbf{v_1},\ldots,\mathbf{v_n})$ una base di $\mathbf{V}$ e si ponga, per ogni $\mu \in \mathrm{K}^{\ast}, \mu \mathcal{B} := (\mu \mathbf{v_0},\ldots, \mu \mathbf{v_n}).$
Sia $\mathbf{v} = (x_0, \ldots,x_n)_{\mathcal{B}};$ allora si ha

4 ESEMPIO Sia $P \in \mathbf{P^2(R)}$ e sia $\mathcal{B} = \mu \mathcal{E}$ con $\mu \in \mathrm{K}^{\ast}.$ Allora $P = [3, 1, 2]_{\mathcal{B}} = [3\mu, \mu, 2\mu]_{\mathcal{E}} = [3, 1, 2]_{\mathcal{E}}.$