riferimenti proiettivi

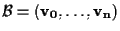
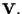
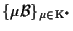
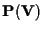
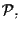
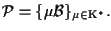
5 DEFINIZIONE Sia $\mathcal{B}=(\mathbf{v_0},\ldots,\mathbf{v_n})$ una base di $\mathbf{V}.$ Diciamo che la famiglia di basi $\{ \mu \mathcal{B} \}_{\mu \in \mathrm{K}^{\ast}}$ definisce in $\mathbf{P(V)}$ un sistema di coordinate omogenee, o riferimento proiettivo, $\mathcal{P},$ cioè $\mathcal{P} = \{ \mu \mathcal{B} \}_{\mu \in \mathrm{K}^{\ast}}.$
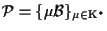
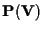
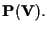
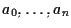
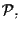
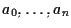
Sia $\mathcal{P} = \{ \mu \mathcal{B} \}_{\mu \in \mathrm{K}^{\ast}}$ un riferimento proiettivo su $\mathbf{P(V)}$ e sia $[\mathbf{v} ]$ un punto di $\mathbf{P(V)}.$ Diciamo che $[\mathbf{v} ]$ ha coordinate omogenee $a_0, \ldots,a_n$ rispetto a $\mathcal{P},$ e scriviamo $[\mathbf{v} ] = [a_0, \ldots,a_n]_{\mathcal{P}},$ se $a_0, \ldots,a_n$ sono le coordinate omogenee di $[\mathbf{v} ]$ rispetto a una qualsiasi delle basi della famiglia $\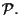mathcal{P}.$ Questa definizione ha senso grazie alla proposizione 3.
Le coordinate omogenee di $[\mathbf{v} ]$ sono determinate, come già visto, a meno di un fattore di proporzionalità.
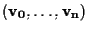
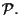
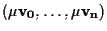
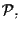
Viceversa, le coordinate rispetto a un riferimento proiettivo determinano il punto; infatti, se $P = [a_0, \ldots,a_n]_{\mathcal{P}},$ allora $P = [ a_0 \mathbf{v_0} + \cdots + a_n \mathbf{v_n}],$ dove $(\mathbf{v_0},\ldots,\mathbf{v_n})$ è una base della famiglia $\mathcal{P}.$ Se consideriamo un'altra base qualsiasi $(\mu \mathbf{v_0}, \ldots, \mu \mathbf{v_n})$ di $\mathcal{P},$ allora

$\begin{displaymath}P = [ a_0 \mu \mathbf{v_0} + \cdots + a_n \mu \mathbf{v_n}] ... ...athbf{v_n})] = [a_0 \mathbf{v_0} + \cdots + a_n \mathbf{v_n}].\end{displaymath}$

Quello che abbiamo fatto è stato sostanzialmente stabilire una corrispondenza biunivoca

$\begin{displaymath}\begin{array}{cccc} \psi_{\mathcal{P}}: & \mathbf{P(V)} & \lo... ...n]_{\mathcal{P}}) & \longmapsto & [a_0, \ldots,a_n] \end{array}\end{displaymath}$

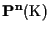
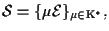
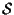
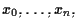
Osserviamo che in $\mathbf{P^n}(\mathrm{K})$ il riferimento proiettivo standard, cioè quello associato alla base canonica, $\mathcal{S} = \{ \mu \mathcal{E} \}_{\mu \in \mathrm{K}^{\ast}},$ fa sí che un punto $[x_0, \ldots,x_n]$ abbia come coordinate omogenee rispetto ad $\mathcal{S}$ proprio $x_0, \ldots,x_n,$ cioè $[x_0, \ldots,x_n] = [x_0, \ldots,x_n]_{\mathcal{S}}.$