Spazi vettoriali euclidei

D'ora in poi porremo, in questo capitolo, $K=\mathbf{R}$.

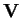
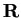
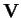
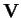
Definizione 1.1   Sia $\mathbf{V} \,$ un $\mathbf{R}$-spazio vettoriale di dimensione finita e $f$ una forma bilineare simmetrica definita positiva su $\mathbf{V}$; allora $f$ è detta prodotto scalare su $\mathbf{V}$.
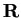
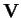
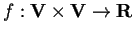
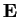
Un $\mathbf{R}$-spazio vettoriale $\mathbf{V}$ con un assegnato prodotto scalare $f:\mathbf{V} \times \mathbf{V} \rightarrow \mathbf{R}$ è detto spazio vettoriale euclideo e d'ora in poi lo denoteremo con $\mathbf{E}$.
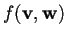
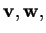
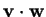
Il prodotto scalare $f(\mathbf{v},\mathbf{w})$ di due vettori $\mathbf{v},\mathbf{w},$ verrá denotato con $\mathbf{v} \cdot \mathbf{w}$ e si leggerà "v scalare w".
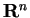
$\mathbf{R}^{n}$ con la forma bilineare standard:

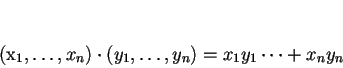 \begin{displaymath} (x_{1},\ldots,x_{n})\cdot(y_{1},\ldots,y_{n}) = x_{1}y_{1}\cdots+x_{n}y_{n} \end{displaymath} (1)

è uno spazio vettoriale euclideo detto n-spazio euclideo.
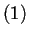
Il prodotto scalare % latex2html id marker 4928 $(\ref{eq:ps})$ è detto prodotto scalare standard.

Teorema 1.2 (Disuguaglianza di Schwartz)  
1.
Se $\mathbf{E}$ è uno spazio vettoriale euclideo di dimensione finita $n$, allora
$\forall \, \mathbf{v},\mathbf{w} \in \mathbf{E}$ si ha:
 \begin{displaymath} (\mathbf{v} \cdot \mathbf{w})^{2} \leq (\mathbf{v} \cdot \mathbf{v})(\mathbf{w} \cdot \mathbf{w}). \end{displaymath} (2)

2.
Inoltre vale l'uguaglianza se e solo se $\mathbf{v}$ e $ \mathbf{w}$ sono linearmente dipendenti.

Dimostrazione