Esempi

1.
Si consideri la forma bilineare simmetrica $f$:
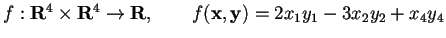
$f:\mathbf{R}^4 \times \mathbf{R}^4 \rightarrow \mathbf{R}, \qquad f(\mathbf{x},\mathbf{y})=2x_{1}y_{1}-3x_{2}y_{2}+x_{4}y_{4}$.
L'applicazione $f$ non è un prodotto scalare, infatti la sua segnatura è (2,1), quindi $f$ non è definita positiva, bensì indefinita.

2.
La forma $f \,$ su $\, \mathbf{R}^3 \times \mathbf{R}^3$:
$f(\mathbf{x},\mathbf{y})=x_{1}y_{1}-3x_{2}y_{2}+4x_{3}y_{3}+x_{1}y_{2}+x_{2}y_{1}+4x_{1}y_{3}+4x_{3}y_{1}$
non è un prodotto scalare, poiché è degenere; infatti, considerando la matrice associata a $f$, si trova facilmente che $r(f)=2$.

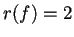3.
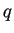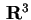Si consideri la forma quadratica $q$ su $\,\mathbf{R}^3$ tale che
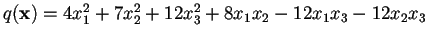
$q(\mathbf{x})=4x_{1}^2+7x_{2}^2+12x_{3}^2+8x_{1}x_{2}-12x_{1}x_{3}-12x_{2}x_{3}$;
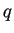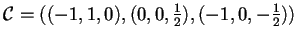allora la forma bilineare simmetrica $f$ associata a $q$ è un prodotto scalare, infatti, presa $\mathcal{C}=((-1,1,0),(0,0,\frac{1}{2}),(-1,0,-\frac{1}{2}))$, base diagonalizzante per $f$, si ha che:
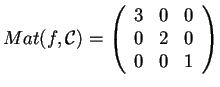
$Mat(f,\mathcal{C})=\begin{array}({ccc}) 3 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{array}$;
quindi la sua segnatura è (3,0).
Questo significa che $f$ è una forma definita positiva.