

- 1.
- Stabilire quali fra le seguenti forme bilineari simmetriche
- a)
-
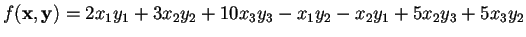 ;
;
- b)
-
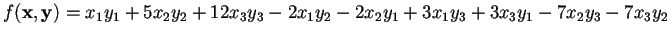 ;
;
- c)
-
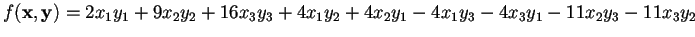 ;
;
è un prodotto scalare sullo spazio euclideo
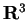 ,
sia utilizzando il criterio dei minori principali , sia calcolando la segnatura di
,
sia utilizzando il criterio dei minori principali , sia calcolando la segnatura di 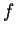 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Ora diagonalizziamo la matrice e calcoliamo la sua segnatura:
prendiamo un vettore non isotropo per la forma bilineare, ad esempio
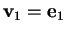 ,
infatti
,
infatti
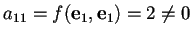 ,
quindi ricordiamo che
,
quindi ricordiamo che
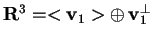 .
.
Passiamo a determinare il sottospazio
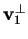 :
:
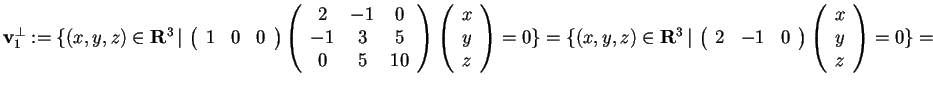
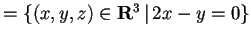
da cui otteniamo
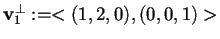 .
.
Scegliamo ora un vettore che appartiene a
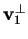 ,
ad esempio
,
ad esempio
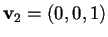 e troviamo
e troviamo
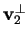 :
:
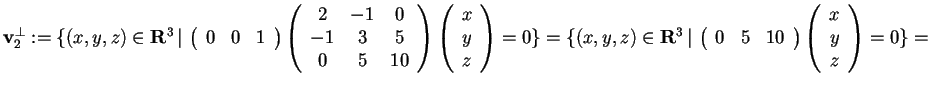
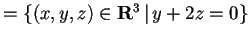
Abbiamo finora scomposto lo spazio euclideo come
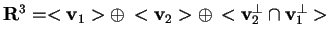
;
Per avere il terzo vettore, basterà fare l'intersezione dei due sottospazi ortogonali, quindi
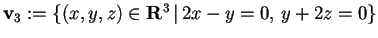
da cui avremo
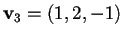 .
.
La base diagonalizzante risulta essere
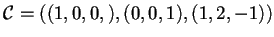 e la matrice associata:
e la matrice associata:
La segnatura è (2,0), quindi 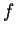 ,
essendo semidefinita positiva, non è un prodotto scalare.
,
essendo semidefinita positiva, non è un prodotto scalare.
Punto
b)
Ora diagonalizziamo la matrice e calcoliamo la sua segnatura:
prendiamo un vettore non isotropo per la forma bilineare, ad esempio
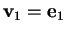 ,
infatti
,
infatti
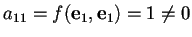 ,
quindi ricordiamo che
,
quindi ricordiamo che
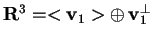 .
.
Passiamo a determinare il sottospazio
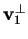 :
:
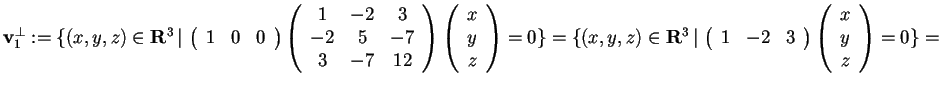
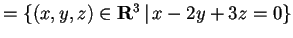
da cui otteniamo
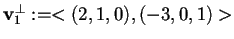 .
.
Scegliamo ora un vettore che appartiene a
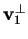 ,
ad esempio
,
ad esempio
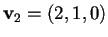 e troviamo
e troviamo
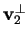 :
:
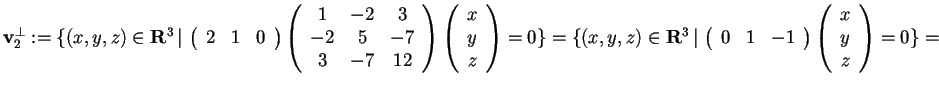
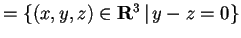
Abbiamo finora scomposto lo spazio euclideo come
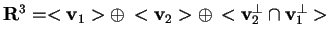
;
Per avere il terzo vettore, basterà fare l'intersezione dei due sottospazi ortogonali, quindi
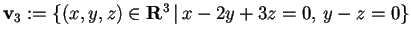
da cui avremo
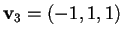 .
.
La base diagonalizzante risulta essere
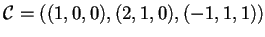 e la matrice associata:
e la matrice associata:
La segnatura è (3,0), quindi  ,
essendo definita positiva, è un prodotto scalare.
,
essendo definita positiva, è un prodotto scalare.
Punto
c)
Ora diagonalizziamo la matrice e calcoliamo la sua segnatura:
prendiamo un vettore non isotropo per la forma bilineare, ad esempio
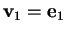 ,
infatti
,
infatti
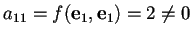 ,
quindi ricordiamo che
,
quindi ricordiamo che
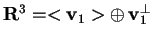 .
.
Passiamo a determinare il sottospazio
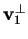 :
:
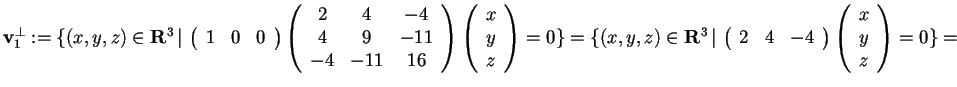
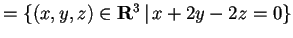
da cui otteniamo
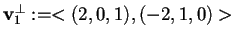 .
.
Scegliamo ora un vettore che appartiene a
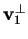 ,
ad esempio
,
ad esempio
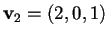 e troviamo
e troviamo
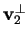 :
:
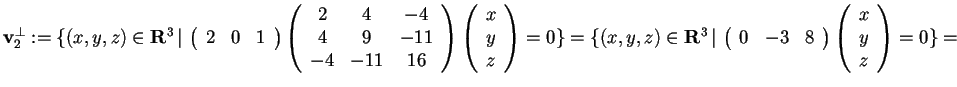
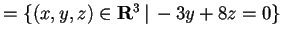
Abbiamo finora scomposto lo spazio euclideo come
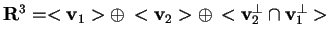
;
Per avere il terzo vettore, basterà fare l'intersezione dei due sottospazi ortogonali, quindi
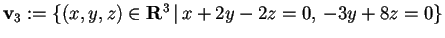
da cui avremo
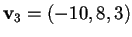 .
.
La base diagonalizzante risulta essere
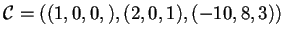 e la matrice associata:
e la matrice associata:
La segnatura è (2,1), quindi 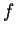 ,
essendo indefinita, non è un prodotto scalare.
,
essendo indefinita, non è un prodotto scalare.





;
;
;
, sia utilizzando il criterio dei minori principali , sia calcolando la segnatura di
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzioneabbiano segno positivo, mentre con il secondo metodo dobbiamo diagonalizzare la matrice e controllare che la sua segnatura sia (3,0); così possiamo concludere che
è una forma definita positiva, e quindi un prodotto scalare su uno spazio euclideo.
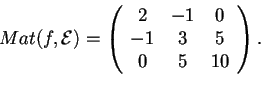
;
;
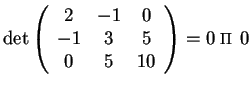
non è un prodotto scalare.
, infatti
, quindi ricordiamo che
.
:
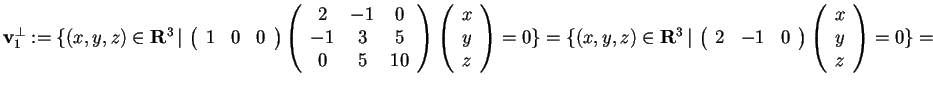
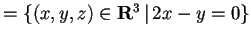
.
, ad esempio
e troviamo
:
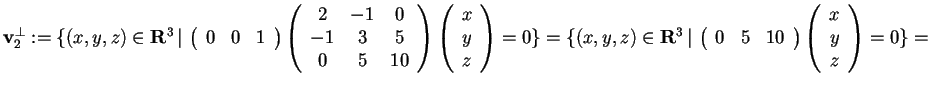
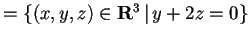
;
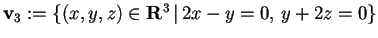
.
e la matrice associata:
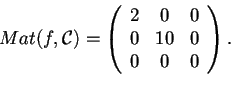
, essendo semidefinita positiva, non è un prodotto scalare.
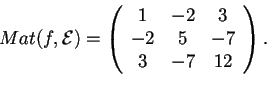
;
;
;
è un prodotto scalare.
, infatti
, quindi ricordiamo che
.
:
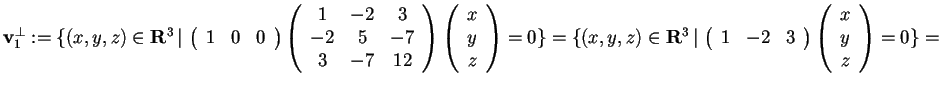
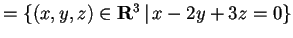
.
, ad esempio
e troviamo
:
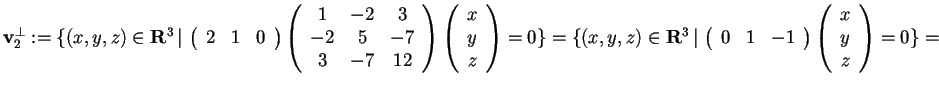
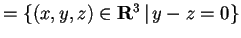
;
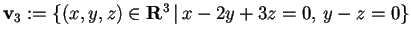
.
e la matrice associata:
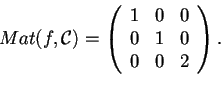
, essendo definita positiva, è un prodotto scalare.
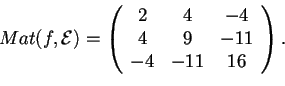
;
;
;
non è un prodotto scalare.
, infatti
, quindi ricordiamo che
.
:
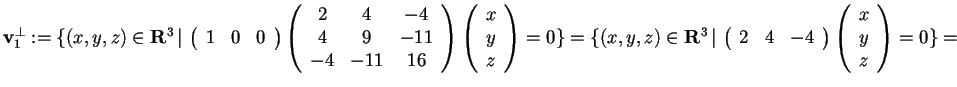
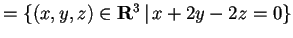
.
, ad esempio
e troviamo
:
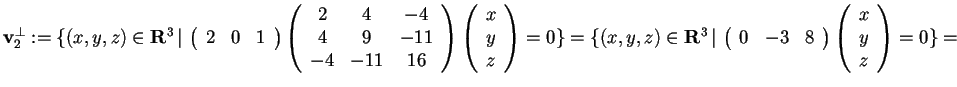
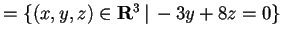
;
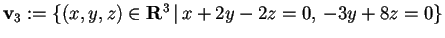
.
e la matrice associata:
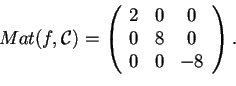
, essendo indefinita, non è un prodotto scalare.



 Teoria
Teoria