Definizione di ortogonalità

Definizione 1.1   Sia $f \in Bils(\mathbf{V})$ e sia $\mathbf{v} \in \mathbf{V}.$
Un vettore $\mathbf{w}$ è detto ortogonale a $\mathbf{v}$ rispetto a f se $f(\mathbf{v},\mathbf{w})=0$.
Allora i vettori $\mathbf{v},\mathbf{w}$ si dicono ortogonali rispetto a $f$ e si scrive anche $\mathbf{v} \perp \mathbf{w}$.

Si noti che la relazione "essere ortogonali" non gode della proprietà transitiva, infatti se $\mathbf{u} \perp \mathbf{v} \,$ e $\, \mathbf{v} \perp \mathbf{w} \, \nRightarrow \quad \mathbf{u} \perp \mathbf{w}$.

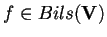
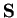
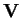
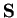
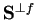
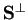
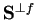
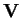
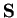
Proposizione 1.2   Supponiamo assegnati $f \in Bils(\mathbf{V})$ e $\mathbf{S}$ sottoinsieme di $\mathbf{V}$. L'insieme dei vettori ortogonali ad ogni elemento di $\mathbf{S}$, si denota $\mathbf{S}^{\perp f}$ (o se non c'è possibilitá di confusione solo $\mathbf{S}^{\perp}$). $\mathbf{S}^{\perp f}$ è un sottospazio vettoriale di $\mathbf{V}$, detto il sottospazio ortogonale o coniugato di $\mathbf{S}$ rispetto a $f$:
$\mathbf{S}^{\perp f}:= \lbrace \mathbf{w} \in \mathbf{V} \quad \vert\quad f(\mathbf{w},\mathbf{v})=0 \quad \forall \mathbf{v} \in \mathbf{S} \rbrace$

Se $\mathbf{S}= \lbrace \mathbf{v} \rbrace$ si scrive $\mathbf{v}^{\perp}$ invece che $\lbrace \mathbf{v} \rbrace^{\perp}$.
Due sottospazi $\mathbf{U,W}$ di $\mathbf{V}$ si dicono ortogonali rispetto a $f$ se $\mathbf{U} \subset \mathbf{W}^{\perp}$.

Dimostrazione

Proposizione 1.3   Sia $f \in Bils(\mathbf{V})$, allora:
$f$ è non degenere $\quad \Longleftrightarrow \quad \mathbf{V}^{\perp}= < 0 >$.

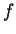
Dimostrazione