Esercizi

1.
Si consideri
$f:\mathbf{R}^3 \times \mathbf{R}^3 \rightarrow \mathbf{R}, \qquad f(\mathbf{x},\mathbf{y})=x_{1}y_{1}-x_{2}y_{2}.$
Si dica se $f$ è degenere oppure no, calcolando $(\mathbf{R}^3)^{\perp}$.

Vuoi un aiuto?
Per vedere la soluzione, clicca

Soluzione
Sappiamo che $f$ non degenere se e solo se $ (\mathbf{R}^3)^{\perp}= <\mathbf{0}>$, quindi andiamo a calcolare quanto vale $(\mathbf{R}^3)^{\perp}$.
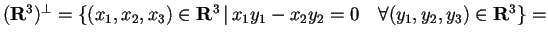
$(\mathbf{R}^3)^{\perp}= \lbrace (x_{1},x_{2},x_{3}) \in \mathbf{R}^3 \, \vert \... ...}y_{1}-x_{2}y_{2}=0 \quad \forall (y_{1},y_{2},y_{3}) \in \mathbf{R}^3 \rbrace=$
$\qquad = \lbrace (x_{1},x_{2},x_{3}) \in \mathbf{R}^3 \, \vert \, x_{1}=x_{2}=0 \rbrace$.
Quindi $(\mathbf{R}^3)^{\perp}= \lbrace (0,0,\alpha) \in \mathbf{R}^3 \, \vert \, \alpha \in \mathbf{R} \rbrace = <(0,0,1)>$, che è diverso dal sottospazio generato dal vettore nullo.
Allora possiamo affermare che $f$ è degenere.