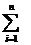Previsione
La previsione o media, attesa, speranza di un
numero aleatorio X esprime l'equivalente certo del fenomeno casuale
rappresentato da X.
Un modo operativo per definire la previsione è il metodo
della scommessa:
Considero X come risultato di una scommessa cioè le perdite o il
guadagno.
Definisco il guadagno G = 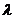 (X
-
(X
- 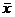 ),
), 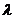
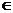
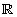 , dove
, dove 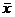 = P(X) rappresenta la previsione di
X, ovvero quel numero reale che rende il guadagno G mai sicuramente
positivo o sicuramente negativo ( Principio di non arbitraggio)
e
= P(X) rappresenta la previsione di
X, ovvero quel numero reale che rende il guadagno G mai sicuramente
positivo o sicuramente negativo ( Principio di non arbitraggio)
e 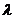 è un coefficiente di
proporzionalità.
è un coefficiente di
proporzionalità.
Da tale definizione discendono le due proprietà della
previsione:
- Proprietà di monotonia inf I(X)

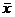
 sup I(X)
sup I(X)
- Proprietà di linearità P(
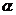 x +
x + 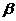 y) =
y) = 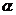 P(X) +
P(X) + 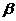 P(Y)
P(Y) 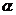 ,
,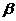
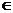
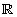
Nel caso di un evento E, la previsione P(E) si dice probabilità
di E. Dalle proprietà di monotonia e linearità, segue
che:
- la probabilità di un evento è un numero compreso
tra 0 ed 1, ovvero 0
 P(E)
P(E)  1;
1;
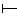 E=1 (E
E=1 (E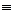 1) => P(E)=1;
1) => P(E)=1; 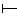 E=0 (E
E=0 (E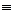 0) => P(E)=0.
0) => P(E)=0.
La funzione che assegna agli eventi di una partizione le loro
probabilità si dice distribuzione di probabilità.
Se E dipende logicamente da una partizione di eventi (E1,E2,...,En)
possiamo trovare la probabilità di E a partire da quella degli Ei.
P(E) = 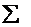 Ei
Ei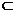 E P(Ei)
E P(Ei)
Vediamo ora un metodo operativo per calcolare la previsione.
Sia X un numero aleatorio con I(X)={x1,...,xn} e
sia Ei := (X = xi).
Si ha che:
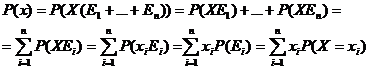
Si noti infatti che XEi è un numero aleatorio che
assume il valore xi oppure 0.
L'uguaglianza P(xiEi)=xiP(Ei)
è una conseguenza della proprietà di linearità
della previsione.
In generale, se 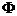 :
: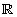
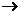
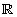 , vale che P(
, vale che P(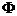 (x))=
(x))=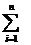
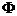 (xi)P(X=xi).
(xi)P(X=xi).
Riassumendo: P(X):= 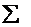 xi xi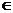 I(X)
xi P(X=i) I(X)
xi P(X=i)
|
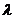 (X
-
(X
- 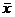 ),
), 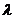
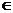
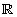 , dove
, dove 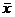 = P(X) rappresenta la previsione di
X, ovvero quel numero reale che rende il guadagno G mai sicuramente
positivo o sicuramente negativo ( Principio di non arbitraggio)
e
= P(X) rappresenta la previsione di
X, ovvero quel numero reale che rende il guadagno G mai sicuramente
positivo o sicuramente negativo ( Principio di non arbitraggio)
e 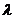 è un coefficiente di
proporzionalità.
è un coefficiente di
proporzionalità.

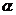 x +
x + 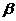 y) =
y) = 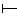 E=1 (E
E=1 (E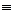 1) => P(E)=1;
1) => P(E)=1;  Ei
Ei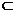 E P(Ei)
E P(Ei) 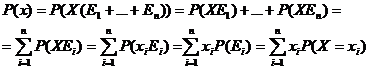
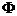 :
: