Allora I(X,Y) = { (i,j) / 1
 i
i 6, 1
6, 1 j
j 6} = I(X) x I(Y).
6} = I(X) x I(Y).
Un numero aleatorio X è una quantità ben definita,
ma non necessariamente nota, che si determina dopo aver effettuato
un esperimento.
Si possono conoscere i valori possibili, cioè i
valori che il numero aleatorio può assumere.
I(X) denota l'
insieme dei valori possibili del numero aleatorio X.
| Esempio Un numero aleatorio può
rappresentare il lancio di un dado I(X) = {1,2,3,4,5,6}
o di una moneta I(X) = {T,C} oppure I(X) = {0,1} indicando "T" (testa) con "0" e "C" (croce) con "1". |
Un vettore aleatorio (X1,X2,...,Xn) è un vettore i cui elementi sono dati da numeri aleatori.
L'insieme dei valori possibili I(X1,X2,...,Xn) del vettore aleatorio è dato dalle n-uple che il vettore può assumere.
Due numeri aleatori X e Y si dicono logicamente indipendenti se
I(X,Y)= I(X) × I(Y) dove I(X) × I(Y) indica il prodotto cartesiano fra l'insieme dei valori possibili I(X) e l'insieme dei valori possibili I(Y).
| Esempio 1
Si consideri il lancio di due dadi.Sia X il numero aleatorio che rappresenta la faccia che esce nel primo dado e sia Y il numero aleatorio che rappresenta l'esito del lancio del secondo dado.
Allora I(X,Y) = { (i,j) / 1  i i 6, 1 6, 1 j j 6} = I(X) x I(Y). 6} = I(X) x I(Y).
|
| Esempio 2
Si consideri un'urna con palline numerate da 1 a 10. Si eseguano due estrazioni con reimbussolamento. Sia X il risultato della prima estrazione e Y il risultato della seconda.
L'insieme dei valori possibili è allora I(X,Y) = { (i,j) / 1  i i 10, 1 10, 1 j j 10}. 10}.
I(X,Y) = I(X) x I(Y) quindi X e Y sono logicamente indipendenti. |
| Esempio 3
Si consideri un'urna con palline numerate da 1 a 10. Si eseguano due estrazioni senza reimbussolamento. Siano X e Y i risultati rispettivamente della prima e della seconda estrazione.
L'insieme dei valori possibili è allora I(X,Y) = { (i,j) / 1  i i 10, 1 10, 1 j j 10, i 10, i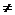 j}. j}.
I(X,Y) 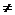 I(X) x I(Y) perchè I(X,Y) non contiene le coppie del tipo (i,j), i I(X) x I(Y) perchè I(X,Y) non contiene le coppie del tipo (i,j), i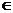 {1,...,10}. {1,...,10}.
I numeri aleatori X e Y non sono logicamente indipendenti. |
Con i numeri aleatori si possono eseguire tutte le consuete operazioni aritmetiche e considerare funzioni di essi.
In particolare si può considerare:
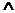 Y = min(X,Y)
Y = min(X,Y)
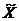 = 1 - X
= 1 - X
Un numero aleatorio X si dice evento se I(X)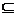 {0,1}.
In particolare, se X è identicamente uguale ad uno
{0,1}.
In particolare, se X è identicamente uguale ad uno
(X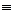 1 oppure
1 oppure 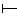 X=1), si parla di evento certo; se X è identicamente uguale ad zero
X=1), si parla di evento certo; se X è identicamente uguale ad zero
(X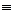 0 oppure
0 oppure 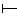 X=0), si parla di evento nullo.
X=0), si parla di evento nullo.
Gli eventi si indicano in generale con lettere del tipo E,F,...
Nel caso degli eventi si parla di operazioni logiche:
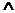 F = EF
F = EF
 = 1 - E
= 1 - E
Consideriamo ora n eventi E1,E2,...,En. Essi si dicono:
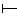 EiEj=0,
EiEj=0, 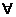 i
i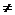 j
j
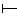 E1+E2+...+En
E1+E2+...+En 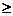 1 (almeno un evento si verifica sempre)
1 (almeno un evento si verifica sempre)
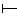 E1+E2+...+En = 1 (si verifica sempre solo un evento)
E1+E2+...+En = 1 (si verifica sempre solo un evento)
| Esempio Si consideri il lancio di un dado. Sia Ei l'evento che corrisponde all'uscita della i-esima faccia. Allora gli Ei danno una partizione perchè esce sempre una faccia e una sola. |
Dati n eventi E1,E2,...,En, un costituente di essi è dato da Q=E1*,E2*,...,En* dove  .
.
I costituenti di n eventi sono 2n e sono incompatibili due a due. In generale, non tutti i costituenti sono possibili.
I costituenti si possono classificare rispetto ad un dato evento E nel seguente modo:
I tipo se Q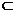 E;
E;
II tipo se Q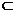
 ;
;
III tipo altrimenti.
Infine E si dice
logicamente dipendente da E1,E2,...,En se tutti i costituenti di E1,E2,...,En sono del primo o del secondo tipo;
logicamente indipendente da E1,E2,...,En se tutti i costituenti di E1,E2,...,En sono del terzo tipo;
logicamente semidipendente da E1,E2,...,En altrimenti.
Esempio 1
Supponiamo di effettuare cinque lanci di una moneta. Sia Ei l'evento che corrisponde all'esito "testa" all'i-esimo lancio. Posto Y=E1+E2+E3+E4+E5, considero l'evento E=(Y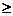 3). 3).
E è semidipendente dai primi tre eventi. Infatti I tipo: E1E2E3 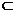 E; E;
II tipo:  1 1 2 2 3 3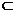  ; ;
III tipo:  1E2 1E2 3 non è contenuto né in E né in 3 non è contenuto né in E né in  . .
|
| Esempio 2
Si consideri un'urna con palline bianche e nere (H palline bianche ed (N-H) palline nere). Si eseguano cinque estrazioni con reimbussolamento. Sia Ei l'evento che corrisponde all'uscita di una pallina bianca all'i-esima estrazione. Sia Y il numero aleatorio che conta le palline bianche ottenute nelle cinque estrazioni:Y=E1+E2+E3+E4+E5.
Considero l'evento E=(Y 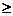 3) e gli eventi E1,E2,E3. 3) e gli eventi E1,E2,E3.
E è semidipendente dai primi tre eventi. Infatti I tipo: E1E2E3 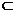 E; E;
II tipo:  1 1 2 2 3 3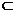  ; ;
III tipo: E1  2E3. 2E3.
|