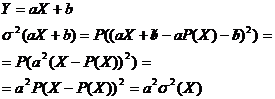Varianza

Dato un numero aleatorio X, si definisce la varianza di X
(X) = P [(X-P(X))²] o equivalentemente (X)=P(X²)-P(X)².
Se la varianza è nulla, allora X è una costante, ovvero tutta la probabilità è concentrata sulla previsione P(X).
Sia I(X)={1,2,...,n}, se X ha distribuzione discreta
P(X)=_i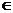I(X)i P(X=i)   e P(X²)=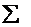_i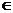I(X) i² P(X=i). La varianza rispetta la seguente proprietà:
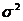(aX+b)=a²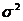(X)

Dimostrazione: