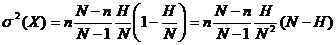Distribuzione ipergeometrica

Si consideri un'urna contenente N palline di cui H bianche ed N-H nere. Si facciano n estrazioni senza reimbussolamento. Sia X il numero aleatorio che rappresenta il numero di palline bianche estratte.
Il numero minimo di palline bianche fra le n estratte sarà pari a 0 se nell'urna le palline nere sono più di n, mentre sarà dato da n-(N-H) se una volta scelte tutte le palline nere rimarranno da determinare ancora degli elementi del campione. Viceversa, il numero massimo delle palline bianche fra le n estratte è dato dal minimo fra n ed il numero massimo di palline bianche nell'urna, ovvero H. Si ottiene che: I(X)={0 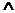n - (N-H),...,n V H}
Sia k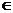I(X). Calcoleremo la distribuzione di probabilità di X utilizzando la formula P(X=k)=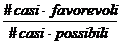
Il numero di casi possibili coincide con il numero di modi di scegliere n palline fra le N presenti nell'urna senza ripetizione e senza tener conto dell'ordine, ovvero #casi possibili=
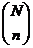
Per avere k palline bianche nel campione, bisogna prendere k palline bianche fra le H contenute nell'urna e scegliere le restanti (n-k) fra le (N-H) nere. Ne segue che #casi favorevoli=

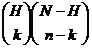
Si dice che X ha distribuzione ipergeometrica e vale che
P(X=k)=()/()
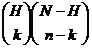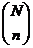Per chiarire il concetto di combinazioni rimandiamo al progetto di CALCOLO COMBINATORIO
Ritornando al nostro caso sia E_k l'evento E_k=(esce una pallina bianca alla k-esima estrazione). La probabilità di ottenere una pallina bianca alla k-esima estrazione è data da
 
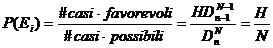
Infatti se si considerano le n palline estratte come ordinate in una n-upla, il numero di casi favorevoli è dato dalle n-uple ordinate che hanno una pallina bianca all'i-esimo posto, mentre il numero dei casi possibili sono tutte le n-uple ordinate di n elementi scelti si N.
Poiché X=E₁+E₂+...+E_n, per calcolare la previsione usando la proprietà di linearità si ottiene P(X)=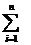P(E_i)=n(H/N)
La varianza della distribuzione ipergeometrica &egrave:

Riassumendo: Distribuzione ipergeometrica Caratteristiche:I(X)={0 n - (N-H),...,n V H} Distribuzione di probabilit&agrave:P(X=k)=()/() Previsione:P(X)=nH/N Varianza: