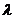 , con
, con 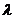 > 0,se:
> 0,se:
Un numero aleatorio X si dice avere distribuzione di Poisson di parametro 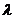 , con
, con 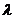 > 0,se:
> 0,se:
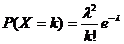
Verifichiamo che sia una distribuzione di probabilità.
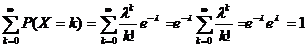
Calcoliamo la previsione di X:
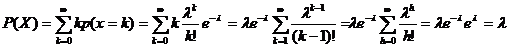
Dove abbiamo posto h=k-1.
Infine calcoliamo la varianza della distribuzione di Poisson.
Ricordando che 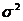 (X)=P(X2)-P(X)2, basta calcolare P(X2).
(X)=P(X2)-P(X)2, basta calcolare P(X2).
Si ottiene:
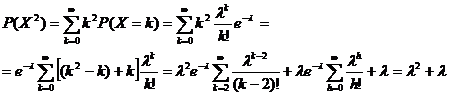
Dove abbiamo posto h=k-2.
Quindi la varianza è data da 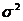 (X)=P(X2)-P(X)2=
(X)=P(X2)-P(X)2=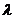 2+
2+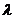 -
-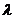 2=
2=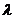 .
.
Riassumendo:
Distribuzione di PoissonCaratteristiche:I(X)=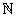 e e 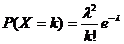 . .
Previsione:P(X)= 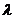
Varianza: 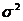 = =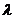
|