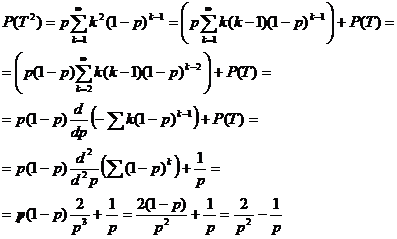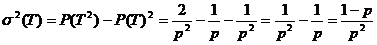Distribuzione geometrica
Sia (Ei)i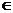
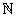 uno schema di Bernoulli e sia T il numero aleatorio che rappresenta l'istante di primo successo in una serie di prove, ovvero
T= inf {n / En=1}.L'insieme dei valori possibili per il numero aleatorio T è dato da: I(T)={1,2,...}=
uno schema di Bernoulli e sia T il numero aleatorio che rappresenta l'istante di primo successo in una serie di prove, ovvero
T= inf {n / En=1}.L'insieme dei valori possibili per il numero aleatorio T è dato da: I(T)={1,2,...}=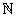 -{0}.
-{0}.
L'evento (T=k) si può scrivere in termini degli Ei come:
(T=k)= 1
1 2...
2... k-1Ek
k-1Ek
Calcoliamo ora la distribuzione di probabilità:
P(T=k)=P( 1
1 2...
2... k-1Ek)=P(
k-1Ek)=P( 1)P(
1)P( 2)...P(
2)...P( k-1)P(Ek)=(1-p)k-1p
k-1)P(Ek)=(1-p)k-1p
Si dice che T ha distribuzione geometrica di parametro p.
Verifichiamo di aver ottenuto una distibuzione di probabilità, cioè che 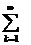 P(T=k)=1. Utilizzando la somma della serie geometrica, otteniamo infatti:
P(T=k)=1. Utilizzando la somma della serie geometrica, otteniamo infatti:
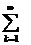 P(T=k)=
P(T=k)=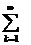 (1-p)i-1p = p
(1-p)i-1p = p 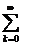 (1-p)k = p/(1-(1-p)) = 1
Tenendo presente che per la serie geometrica
(1-p)k = p/(1-(1-p)) = 1
Tenendo presente che per la serie geometrica 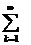 xk vale
xk vale 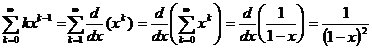
calcoliamo la previsione di T: P(T)=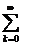 k P(T=k) =
k P(T=k) = 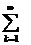 k(1-p)k-1p = p
k(1-p)k-1p = p 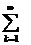 k(1-p)k-1 = p (1/p2)= 1/p
k(1-p)k-1 = p (1/p2)= 1/p
La distribuzione geometrica gode della proprietà di assenza di memoria, cioè la probabilità di avere un successo dopo m+n prove, se non si è ottenuto successo nelle prime n prove, non dipende dalle prime n prove.
Possiamo anche enunciarla così: P( T > m+n / T > n ) = P( T > m )
Infine calcoliamo la varianza della distribuzione geometrica.
Ricordando che 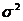 (X)=P(X2)-P(X)2,
(X)=P(X2)-P(X)2,
basta calcolare P(T2)=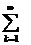 k2p(1-p)k-1.
k2p(1-p)k-1.
Si ottiene
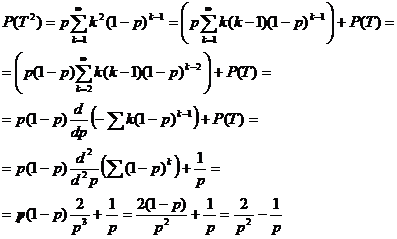
Quindi
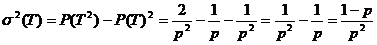
Riassumendo:
Distribuzione geometrica
Caratteristiche: Schema di Bernoulli e I(T)=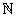 -{0}. -{0}.
Distribuzione di probabilità: P(T=k)=(1-p)k-1p
Previsione:P(T)=1/p
Varianza: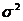 (T)= (1-p)/p2 (T)= (1-p)/p2
|
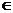
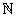 uno schema di Bernoulli e sia T il numero aleatorio che rappresenta l'istante di primo successo in una serie di prove, ovvero
T= inf {n / En=1}.L'insieme dei valori possibili per il numero aleatorio T è dato da: I(T)={1,2,...}=
uno schema di Bernoulli e sia T il numero aleatorio che rappresenta l'istante di primo successo in una serie di prove, ovvero
T= inf {n / En=1}.L'insieme dei valori possibili per il numero aleatorio T è dato da: I(T)={1,2,...}=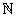 -{0}.
-{0}.
 1
1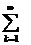 P(T=k)=1. Utilizzando la somma della serie geometrica, otteniamo infatti:
P(T=k)=1. Utilizzando la somma della serie geometrica, otteniamo infatti:
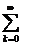 (1-p)k = p/(1-(1-p)) = 1
Tenendo presente che per la serie geometrica
(1-p)k = p/(1-(1-p)) = 1
Tenendo presente che per la serie geometrica 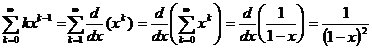
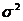 (X)=P(X2)-P(X)2,
(X)=P(X2)-P(X)2,