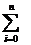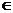
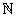 uno schema di Bernoulli e sia X il numero aleatorio che conta il numero di successi avvenuti nelle n prove.
uno schema di Bernoulli e sia X il numero aleatorio che conta il numero di successi avvenuti nelle n prove.
X si può scrivere come P(Ei)=p
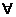 i
i 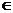
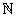 , con 0 < p < 1 = il numero di successi su n prove.
, con 0 < p < 1 = il numero di successi su n prove.
L'insieme dei valori possibili di X è quindi I(X)={0,...,n}.
Calcoliamo, attraverso i costituenti, la distribuzione di probabilità di X.
Per
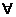 k
k 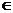 {0,...,n}, si ha che
{0,...,n}, si ha che
P(X=k)=P(
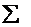 Q
Q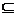 EQ) dove Q è un costituente di I tipo dell'evento E
EQ) dove Q è un costituente di I tipo dell'evento E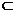 Q.
Q.
Tutti i costituenti di I° tipo contengono k eventi che si verificano ed (n-k) eventi che non si verificano.
Ad esempio Q=E1E2...Ek
 k+1...
k+1... n.
n.
Si osserva che tutti i costituenti di I° tipo per E hanno la stessa probabilità:
P(Q)=P(E1E2...Ek
 k+1...
k+1... n)=P(E1)P(E2)...P(Ek)P(
n)=P(E1)P(E2)...P(Ek)P( k+1)...P(
k+1)...P( n) =
n) =
= pp...p(1-p)...(1-p) = pk(1-p)n-k.
Ora ci resta solo contare quanti sono tali costituenti: essi sono
 ,pari al numero di modi di scegliere i k posti degli eventi che si verificano nella sequenza degli n eventi che compongono il costituente stesso. Si ottiene quindi:
P(X=k)=
,pari al numero di modi di scegliere i k posti degli eventi che si verificano nella sequenza degli n eventi che compongono il costituente stesso. Si ottiene quindi:
P(X=k)=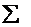 Q
Q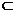 EP(Q)=
EP(Q)=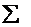 Q
Q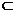 Epk(1-p)n-k =
Epk(1-p)n-k =  pk(1-p)n-k
pk(1-p)n-k
Si dice che X ha distribuzione binomiale
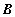 (n,p) di parametri n,p.
(n,p) di parametri n,p.
Verifichiamo di aver ottenuto una distribuzione di probabilità, cioè che
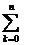 P(X=k)=1. Utilizzando le proprietà del binomio di Newton, otteniamo infatti:
P(X=k)=1. Utilizzando le proprietà del binomio di Newton, otteniamo infatti:
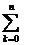 P(X=k)=
P(X=k)=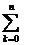
 pk(1-p)n-k=(p+1-p)n= 1
pk(1-p)n-k=(p+1-p)n= 1
Calcoliamo la previsione di X sapendo che X=E1+E2+...+En:
P(X)=P(E1+E2+...+En)=
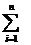 P(Ei)= np
P(Ei)= np
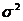 (E1+E2+...+En)=
(E1+E2+...+En)=