Nel capitolo Proprietà dei limiti di successioni abbiamo visto che, per sfruttare le proprietà sui limiti riguardanti le quattro operazioni elementari (+, -,x, /), occorre una certa cautela nel trattare i casi in cui almeno una delle successioni diverge. Infatti, nel teorema relativo a queste proprietà, nulla è stato dimostrato, ad esempio, nel caso in cui una successione  diverga a  e un’altra  diverga a  e si voglia calcolare .

Infatti, a seconda dei singoli esempi, come vedremo, tale limite può convergere oppure divergere o anche può non esistere. Una successione come quella appena costruita la chiameremo forma indeterminata. 

Una forma indeterminata è un tipo di successione tale che, pur essendo ottenuta senza ambiguità da altre successioni mediante le quattro operazioni elementari, non è possibile determinare una formula generale per calcolarne il limite.

In particolare, i casi “critici” si hanno unicamente quando si vuole calcolare il limite di una successione ottenuta mediante la somma o il prodotto o la divisione di due successioni e quando almeno una delle due diverge e l’altra successione diverge o converge a 0.

Vediamo ora una tabella che chiarisce queste osservazioni e che mostra in dettaglio tutte le forme indeterminate. Si consiglia di confrontare questa tabella con quella del capitolo corrispondente sui limiti delle funzioni reali presente in questo stesso sito.

Schematicamente, dunque, le forme indeterminate si classificano in questo modo:

 -         forma indeterminata di tipo

-         forma indeterminata di tipo  

 -         forma indeterminata di tipo

 -         forma indeterminata di tipo

 Si osservi che, ogni volta che si è presentata l’occasione, si è implicitamente supposto che la divisione potesse essere effettuata (cioè che il termine della successione da dividere fosse del tipo ).

     Si può notare che i vari tipi di forme indeterminate si possono ricondurre alla forma . Infatti, se le successioni  e  sono divergenti (positivamente o negativamente), allora, nel caso in cui ogni loro termine sia diverso da 0, la successione  della forma  si può scrivere come:

 ,  (che è della forma ).

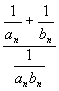 Alle stesse condizioni, se  e  sono divergenti (esattamente una positivamente e l’altra negativamente), la successione  della forma  si può vedere come  che è della forma .

 Infine, analogamente, la successione  con  e  (o viceversa),che è della forma , si può scrivere come  che è della forma .

Concludiamo mostrando come risolvere un tipo particolare di successione che può portare a forme indeterminate, ma che è di facile soluzione in ogni caso. Quando si presenta, cioè, una successione del tipo seguente:

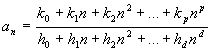
allora, a seconda dei gradi p e d dei polinomi rispettivamente al numeratore e al denominatore, la successione può avere limite finito o infinito.

In particolare, si ha che:

 1)     se , allora, se 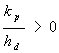, , mentre, se , ;

 2)     se , allora ; 

 3)     se , allora .

 Infatti, per questi casi è sufficiente raccogliere i termini  e  rispettivamente al numeratore e al denominatore, cioè scrivere:

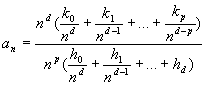
Si possono così applicare, dopo le opportune semplificazioni, le proprietà sui limiti già viste.

Si noti che queste osservazioni si possono generalizzare anche a funzioni reali che hanno la stessa struttura dei polinomi, ma che hanno esponenti reali, non necessariamente interi.

Negli esempi seguenti chiariremo sia le questioni relative all’impossibilità di trovare una formula generale per il calcolo dei limiti con forme indeterminate, sia la risoluzione del tipo di successioni appena mostrato.

ESEMPI (7.1)