Sezione: Elementi di calcolo vettoriale
Se
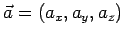 e
e
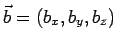 sono due vettori è naturale definire la loro somma come
Geometricamente, se si rappresentano
sono due vettori è naturale definire la loro somma come
Geometricamente, se si rappresentano 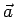 e
e 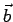 nella forma
nella forma
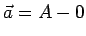 e
e
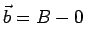 , come vettori spiccati dall' origine, allora
il vettore
, come vettori spiccati dall' origine, allora
il vettore
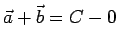 è rappresentato dalla diagonale spiccata dall' origine del parallelogramma generato da
è rappresentato dalla diagonale spiccata dall' origine del parallelogramma generato da 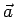 e
e 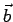 come in figura:
come in figura:
Figura 1.4:
Somma di vettori
|
|
Questa definizione di somma gode delle proprietà commutativa e associativa; ovviamente
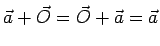 ,
,
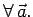 Dalla definizione di somma di vettori e dalla sua rappresentazione geometrica è facile verificare la seguente relazione tra i vettori:
Dalla definizione di somma di vettori e dalla sua rappresentazione geometrica è facile verificare la seguente relazione tra i vettori:
che si può ottenere formalmente "`cancellando"' 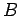 con
con 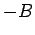 . Questa relazione può anche essere riscritta come:
ed è nota come "relazione di Charles": ovvero nella somma di due vettori "`consecutivi"' si elimina il punto intermedio.(Vedi fig.1.4)
. Questa relazione può anche essere riscritta come:
ed è nota come "relazione di Charles": ovvero nella somma di due vettori "`consecutivi"' si elimina il punto intermedio.(Vedi fig.1.4)
Osservazione 1.1
Il prodotto di un numero per una somma di vettori vale la somma dei singoli vettori moltiplicati per quel numero, cioè
![]() ,
,
![]() Dalla definizione di somma di vettori e dalla sua rappresentazione geometrica è facile verificare la seguente relazione tra i vettori:
Dalla definizione di somma di vettori e dalla sua rappresentazione geometrica è facile verificare la seguente relazione tra i vettori: