 Z*.
Z*.
| Q = { ..., -3/4,..., -2,..., -1,..., -1/3,.., 0,...,1/2,...2/3,...1,...,3/2,...,2,...,15/7,...} |
Vediamo (piuttosto sommariamente) come si può costruire l'insieme dei razionali.
Consideriamo le coppie di interi con il secondo elemento diverso da 0;
ad esempio coppie del tipo (1, -3) , (5,4) ….. , escludendo cioè le coppie del tipo
(1, 0) , (5,0) , (-25, 0). Se indichiamo con Z* = Z \ {0}, stiamo considerando l'insieme Z  Z*.
Z*.
 Z*, raggruppando in una stessa
classe gli elementi (a, b) e (c,d) ogni volta che ad = bc; ad esempio
saranno nella stessa classe gli elementi (3, 2) e
(6, 4) perché 3
Z*, raggruppando in una stessa
classe gli elementi (a, b) e (c,d) ogni volta che ad = bc; ad esempio
saranno nella stessa classe gli elementi (3, 2) e
(6, 4) perché 3
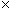 4 = 2
4 = 2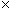 6; possiamo individuare un’altra classe prendendo gli
elementi (-3, -2) e (15, 10) perché -3
6; possiamo individuare un’altra classe prendendo gli
elementi (-3, -2) e (15, 10) perché -3
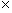 10 = -2
10 = -2
 15, in quest’ultima classe troviamo ad esempio anche l’elemento (21, 14).
15, in quest’ultima classe troviamo ad esempio anche l’elemento (21, 14).  Z*. Possiamo visualizzare tale partizione nel piano cartesiano, notando che le classi sono individuate tramite delle rette
passanti per l’ origine:
Z*. Possiamo visualizzare tale partizione nel piano cartesiano, notando che le classi sono individuate tramite delle rette
passanti per l’ origine:
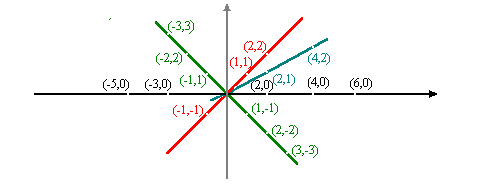
Chiamiamo Q l’ insieme quoziente di questa partizione, e quindi consideriamo come "nuovi numeri" le classi della partizione sopra considerata. Tali elementi saranno i nostri numeri razionali.
Useremo il simbolo a/b per indicare la
classe della coppia (a, b).
Ad esempio se prendiamo gli elementi (-3, 3) ed (-1,
1) , essi appartengono alla stessa classe e quindi avremo che
–3/3 = -1/1 ; lo stesso accade per (3, 2) e (6,
4)
che appartengono ad una stessa classe e quindi 3/2 =
6/4 (ma diversa
dalla classe precedente).
Poiché esistono più modi per indicare uno stesso elemento razionale, in generale
si preferisce usare la notazione a/b ove a e b siano primi tra loro (cioè a e b non
hanno fattori in comune) e b > 0. In questo caso si dice che la frazione è ridotta ai minimi termini .
Ad esempio 3/2 oppure 1/2, o ancora 1/3 sono frazioni ridotte ai
minimi termini mentre 2/4 , 3/-9 e 2/-5 sono frazioni non ridotte ai minimi termini. Per trasformarle
in frazioni ridotte ai minimi termini dobbiamo scriverle come: 1/2 , -1/3 e -2/5.
Una volta definito Q come insieme, dobbiamo definire le operazioni in esso; l'addizione e la moltiplicazione le definiamo nel modo seguente:
1) Se a/b , c/d  Q : (a/b) + (c/d) = (ad +bc)/bd ;
Q : (a/b) + (c/d) = (ad +bc)/bd ;
2)
Se a/b , c/d  Q : (a/b)
Q : (a/b)
![]() (c/d) = ac/bd ;
(c/d) = ac/bd ;
Notiamo che le operazioni sono ben definite cioè che se invece di a/b utilizziamo un’altra espressione per rappresentare la stessa classe (ad esempio 3a/3b ), il risultato delle operazioni è sempre lo stesso, infatti:
(3ad + 3bc)/3bd = (ad +bc)/bd ;
(3ac)/(3bd) = ac/bd;
Esempi
3/9 + 16/12 = 4/12 + 16/12 = 20/12 ; 3/7 + (-1/3) = [9+(-7)]/21 = 2/21 ; 4/1 + 0/211 = (844+0)/211 = 4/1 ;
3/5 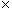 7/9 = 21/45 = 7/15 ; 12/12
7/9 = 21/45 = 7/15 ; 12/12 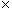 3/8 = 36/96 = 3/8
; -2/9
3/8 = 36/96 = 3/8
; -2/9 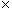 12/5 = -24/45 = -8/15
; -4/3
12/5 = -24/45 = -8/15
; -4/3 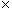 -1/3 = 4/9;
-1/3 = 4/9;
Inoltre si ha, da quanto definito sopra:
3) Se a/b  Q: a/b + 0/1 = a/b
Q: a/b + 0/1 = a/b
4) Se a/b  Q: a/b
Q: a/b 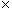 1/1 = a/b
.
1/1 = a/b
.
 N, scriveremo a invece di a/1, e quindi denoteremo con 0 ed 1 gli elementi neutri rispetto alla somma ed al prodotto anche in Q, come in N ed in Z.
N, scriveremo a invece di a/1, e quindi denoteremo con 0 ed 1 gli elementi neutri rispetto alla somma ed al prodotto anche in Q, come in N ed in Z.
 Q : (a/b) - (c/d) = (ad - bc)/bd .
Q : (a/b) - (c/d) = (ad - bc)/bd . Q, se r è diverso da 0, esiste un numero s
Q, se r è diverso da 0, esiste un numero s  Q tale che:
Q tale che: 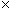 s = s
s = s 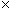 r = 1 .
r = 1 . 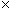 b/a = ab/ab = 1/1 = 1 .
b/a = ab/ab = 1/1 = 1 . 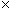 d/c, infatti si ha:
d/c, infatti si ha: 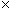 c/d = (a/b
c/d = (a/b 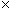 d/c)
d/c) 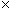 c/d = a/b
c/d = a/b 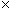 (d/c
(d/c  c/d) = a/b
c/d) = a/b  1 = a/b .
1 = a/b .