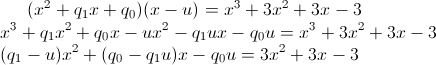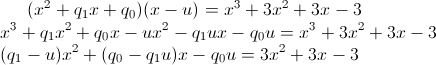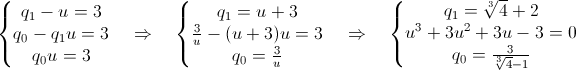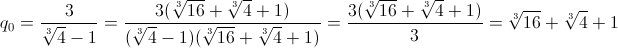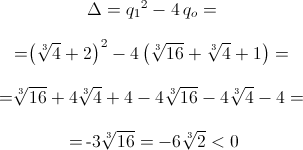Soluzione 5.


  1. Si ha: u=∛4-1 ⇒ u+1=∛4 ⇒ (u+1)3=4 ⇒ u3+3u2+3u-3=0
Il polinomio x3+3x2+3x-3 è a coefficienti razionali, monico, irriducibile (per Eisenstein, p=3) e si annulla in u, dunque è il polinomio minimo di u su Q:
pu(x)=x3+3x2+3x-3
  1. Poichè in R[x] pu(u)=0, pu è divisibile per x-u quindi r=0. Inoltre, essendo pu(x) ed x-u monici, è monico anche q(x). Infine q è necessariamente di grado 2, essendo pu di grado 3 ed x-u di grado 1. Si ha allora che: q(x)=x2+q1x+q0. Svolgendo i conti:


da cui:


Infine per q0 si ha:



  1. Poichè q è un polinomio di secondo grado, si ha che q è irriducibile in R se e solo se il discriminante è strettamente negativo:


da cui q(x)=x2+(∛4+2)x+2∛2+∛4+1 è irriducibile in R[x].


Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 6.