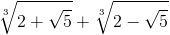
Si ha:
u=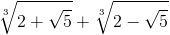
⇓
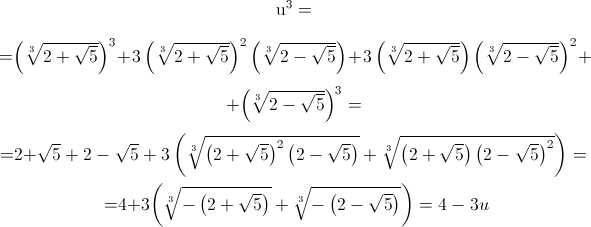
Da qui si ricava il polinomio a coefficienti razionali pu(x)=x3+3x-4 che è monico e si annulla in u. Per poter affermare che x3+3x-4 è il polinomio minimo di u su Q, bisogna provare che esso è irriducibile su Q.
Irriducibilità del polinomio. Un polinomio di terzo grado a coefficienti razionali riducibile ha necessariamente un fattore lineare, esso può infatti spezzare nel prodotto di tre polinomi lineari oppure nel prodotto di uno lineare e uno quadratico irriducibile. Quindi, se non ha neppure una radice razionale è irriducibile su Q, mentre se ne ha almeno una è riducibile.
Ma x3+3x-4 ha 1 come radice; eseguendo la divisione di x3+3x-4 per x-1 si trova: x3+3x-4=(x-1)(x2+x+4). Le due radici di x2+x+4 sono (-1±i√15)/2, quindi non sono reali. Cosa succede? Il polinomio di terzo grado x3+3x-4 si annulla su 1, su u e su due numeri non reali. Dato che non può avere quattro radici, ne segue che:
1=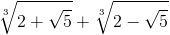
Quindi il polinomio minimo di u=1 su Q è x-1.
Torna agli esercizi.
Torna alla teoria.
Vai all'esercizio 5.
