Soluzione 28.

Si ha, posto ω=cos(2π/6)+i·sen(2π/6): U₆={1, ω, ω², ω³, ω⁴, ω⁵} e con il prodotto questo è un gruppo ciclico isomorfo a (Z₆ , +).

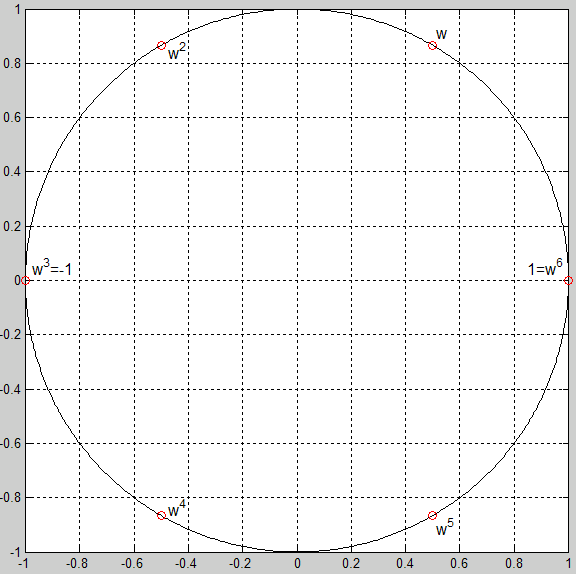
Come mostra la figura sopra:

• ω e ω⁵ hanno periodo 6, infatti 1 e 5 sono coprimi con 6; le radici con questi indici hanno periodo massimo e ciascuna genera da sola tutto U₆ (ω e ω⁵ radici seste primitive).
• ω² e ω⁴ hanno periodo 3 ((2,6)=2=(4,6)), essendo anche radici cubiche di 1.
• ω³=-1 ha periodo 1, essendo questa anche radice quadrata di 1.
• ω⁶=1 ha periodo 1, da cui: [Q(ω⁶):Q]=[Q:Q]=1.

Inoltre ω⁴ è uguale al complesso coniugato di ω² e ω⁵ al complesso coniugato di ω. Tutte sono radici di x⁶-1 che fattorizza così: x⁶-1=(x-1)(x+1)(x²-x+1)(x²+x+1).

• 1 e ω³=-1 hanno grado 1 su Q perchè sono già in Q.
• ω⁴=(-1-i√3)/2 e ω²=(-1+i√3)/2 sono radici del polinomio x²+x+1 che è irriducibile su Q perchè è senza radici in Q.
• ω=(1+i√3)/2 e ω⁵=(1-i√3)/2 sono radici del polinomio x²-x+1 che è irriducibile su Q perchè è senza radici in Q.

Quindi il grado di ω, ω², ω⁴, ω⁵ è 2.

Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 29.