FUNZIONE
LOCALMENTE LIPSCHITZIANA
DEFINIZIONE: Sia ( t, u )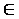
A
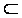
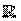n+1. Una funzione
f : A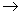 
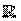n si dice localmente lipschitziana su A rispetto a u se per ogni insieme convesso compatto K
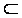A esiste una costante L>0 tale che:
| f
( t, u1 ) - f ( t,
u2 ) | 
L | u1
- u2 | per ogni ( t, u1 ), ( t, u2
) 
K
OSSERVAZIONE :
Se f ha derivate parziali limitate, allora è
localmente lipschitziana.
Se f ha derivate parziali continue, allora è
localmente lipschitziana.
|
|
|
|
