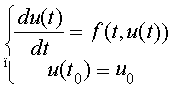PROBLEMA DI CAUCHY
Sia A un aperto di 
n+1; sia f una funzione continua da A in n: in simboli, f
C ( A, n ).
Sia ( t, u ) 
n+1
con t 
,
u 
n
e (to , u0) 
A.
Il problema di Cauchy
consiste nel trovare un intervallo [to-d, to+d] ed una
funzione u: [to-d, to+d]
n t.c:
essendo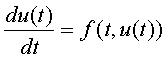 
equazione
differenziale del primo ordine.
Esempio:
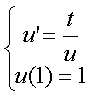
f : A
, f (t ,
u)= t/u , (t0, u0)
= (1,1)
|
|
|
|
