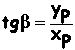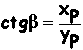Le funzioni nelle quali la variabile indipendente è un angolo (o un arco) vengono dette goniometriche o circolari.
Per definire le funzioni goniometriche elementari si consideri fisso il lato di origine degli angoli (identificato, nel caso del riferimento cartesiano ortogonale xOy, col semiasse positivo delle ascisse) e variabile il secondo.
Si consideri ora nella seguente figura l'angolo orientato b il cui primo lato coincide appunto col semiasse positivo delle ascisse e il secondo è la semiretta r:
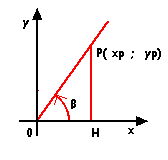
Sia P un generico punto della semiretta r,siano xp e yp le sue coordinate e sia OP la distanza assoluta di P dall'origine O. I quattro rapporti:
|
|
|
|
|
|
SENO DI b
|
COSENO DI b
|
|
TANGENTE DI b
|
COTANGENTE DI b
|
Come si può facilmente verificare, tra le dette quattro funzioni di uno stesso angolo b intercorrono le seguenti relazioni:
![]()
![]()
![]()
![]()
INTERPRETAZIONE
GONIOMETRICA DEL COEFFICIENTE ANGOLARE DI UNA
RETTA