Topologia e spazio topologico

 

Definizione 1.1 Sia X un insieme non vuoto.
Una struttura topologica, o topologia su X è una famiglia t di sottoinsiemi di X tale che valgano le seguenti proprietà:

  1. l’insieme vuoto e X appartengono a t;
  2. l’unione di una qualunque famiglia di elementi di t appartiene ancora a t;
  3. l’intersezione di un numero finito di elementi di t appartiene ancora a t.

Gli elementi di t sono aperti della topologia t.

 

           Esempio

 

Definizione 1.2 Uno spazio topologico è una coppia (X, t) dove X è un insieme non vuoto e t è una topologia su X.
Gli elementi di X sono detti punti

 

Definizioni 1.3 Sia X un insieme non vuoto:
  t = {Æ, X} è detta topologia banale su X;
  t = P (X), dove P(X) è l’insieme delle parti di X, è detta topologia discreta su X;
  k = {Æ}È {A ÍX | X\A è finito} è una topologia detta topologia cofinita su X.

 

           Esempio

 

Osservazione 1.4 In generale, fissato un insieme X, la topologia cofinita e quella discreta sono diverse.
Sono uguali se e solo se X è finito

 

           Esempio

 

Definizione1.5 Definiamo il sottoinsieme di Rn:

Dr(c) = {(x1, …, xn) Í Rn | (x1 - c1)2+…+(xn - cn)2 < r2}
chiamato disco aperto di centro c = (c1,…, cn) e raggio r.

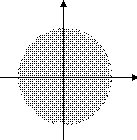
D1 ((0, 0)) Í R2

 

Definizione 1.6 Su Rn definiamo una topologia i cui aperti sono tutte le unioni di dischi aperti, questa topologia è detta topologia euclidea e la denotiamo con e

Per esercizio, dimostrare che e è una topologia

 

           Esempio

 

Gli aperti di e sono unione di dischi aperti:

 

Definizione 1.7 Siano t e t’ due topologie su un X, diciamo che t è meno fine di t’
(scriviamo t <t') se tutti gli aperti di t sono aperti di t’ Se t <t’ è falsa ed è falsa anche t'< t, diciamo che t e t’ non sono confrontabili.

 

 

Esempi Esercizi