Esempi sulle topologie e gli spazi topologici
X =
{1,
2, 3, 4, 5, 6, 7} la famiglia di sottoinsiemi di X: {Æ, X,
{1,
2}, {3}, {1, 2, 3}} è una topologia. Infatti Æ, X appartengono alla famiglia ed è immediato
vedere che l’unione e l’intersezione di una qualunque famiglia di elementi
della famiglia, appartiene ancora ad essa.
Esempio 2
X =
{a, b, c, d}; t1
= {X, Æ,
{a}, {a,
b}, {a,
c, d}};
t2
= {X, Æ, {a},
{c, d},
{a, c,
d}};
le famiglie t1
e t2
sono
topologie, mentre:
t3
= {X, Æ,
{a, b, c}, {b, c, d}} non è una topologia perché
{a,
b, c}Ç {b,
c, d}
Ï
t3;
t4
= {X, Æ,
{b, c},
{a, b, c}, {c, d}} non è una topologia
perché
{b, c} Ç
{c, d}
Ï t4;
t5
= {Æ,
{b}, {b, c}, {b, c,
d}} non è una topologia
perché X Ï t5.
Esempio 3
Siano l'insieme X = {a, b,
c, d}
e la famiglia di sottoinsiemi di X: t1
= {X, Æ,
{a}, {a,
b}, {a,
c, d}},
allora è
facile vedere che (X, t1) è uno spazio topologico.
Esempio 4
Siano l'insieme X = {1, 2, 3, 4, 5, 6, 7} e la famiglia di sottoinsiemi di X:
t = {X,
Æ,{1, 2}, {3}, {1, 2, 3}}, allora è facile vedere che (X,
t)
è uno
spazio topologico.
Sia X = {1,
2, 3};
la topologia banale su X è t1
= {Æ,
X};
la topologia discreta su X è t2
= {Æ, X, {1}, {2}, {3}, {1,
2}, {1, 3}, {2, 3}};
la topologia cofinita su X è t3 = t2
infatti,
essendo X finito, ogni elemento di t2
ha come
complementare in X un insieme finito.
Esempio 6
La famiglia di sottoinsiemi di R costituita da: Æ, R e dagli intervalli (a, +¥)
con aÎR è una topologia su R.
Esempio 7
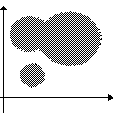
L’insieme {(x, y) Î R2;
(x-3)2 + (y-3)2 < 1 oppure (x-3)2
+ (y-7)2 < 4 oppure (x-6)2 + (y-6)2
< 9}
è un aperto in R2 con la topologia euclidea, perché è
unione di dischi aperti.
Esempio 8
Sia t una qualunque topologia
su un insieme X, la topologia banale
su X è meno fine di t.
Sia k la topologia
discreta su X, allora una qualunque
topologia t su X è meno fine di
k.
Esempio 9
Sia X = {a, b,
c, d}
e siano t = {X,
Æ,
{a}, {a, c, d}} e s = {X, Æ, {a},
{c, d},
{a, c,
d}} due topologie su X, allora t è meno fine di s.
Esempio 10
Sia X = {a, b, c,
d} le topologie su X
t1
= {X, Æ, {a},
{a, b},
{a, c,
d}} e t2
= {X, Æ, {a},
{c, d},
{a, c,
d}} non sono confrontabili.