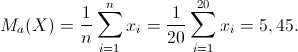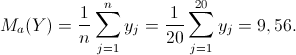ESERCIZIO 3 |
| |
La seguente tabella riporta in forma di distribuzione unitaria doppia i dati delle regioni italiane relativamente al Quoziente di nuzialità (matrimoni per 1000 abitanti) e al Quoziente di natalità (nati per 1000 abitanti).
|
|
| |
 |
| |
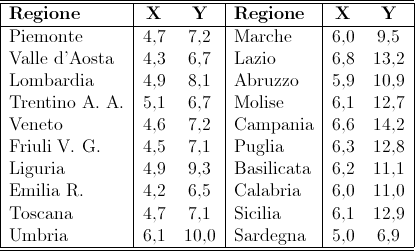
1. Formulare statisticamente la situazione considerata individuando: il collettivo in esame, la sua numerosità, la singola unità statistica, i caratteri considerati e la loro tipologia. |
|
| |
Soluzione del punto 1:
U: Collettivo formato dalle 20 regioni d'Italia; ogni regione rappresenta la singola unità statistica.
La numerosità del collettivo è n=20.
I caratteri considerati sono: X=Quoziente di nuzialità (matrimoni per 1000 abitanti); Y=Quoziente di natalità (nati per 1000 abitanti). I due caratteri sono di tipo quantitativo continuo.
|
| |
2. Si calcoli il baricentro e si disegni il grafico di dispersione relativo alle distribuzioni unitarie dei due caratteri. |
|
| |
Soluzione del punto 2:
Data la distribuzione unitaria doppia di due caratteri X e Y quantitativi, si definisce baricentro la coppia  data dalle medie aritmetiche dei due caratteri.
Per calcolare le due medie aritmetiche utilizziamo quindi le seguenti formule:
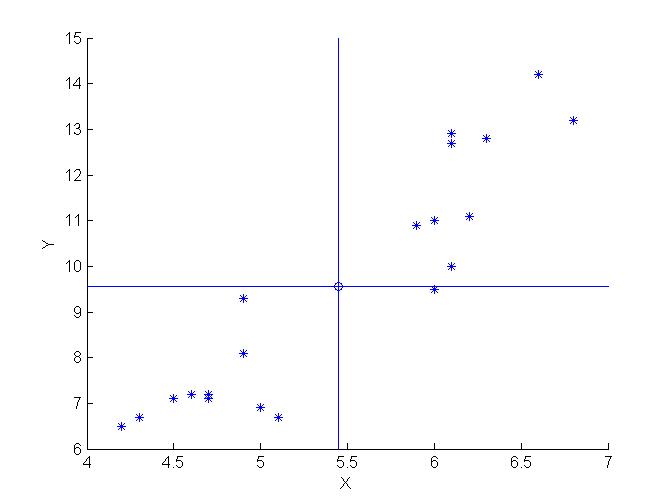
Disegniamo ora il grafico di dispersione:
|
|
| |
3. Si calcoli la covarianza e si commenti il risultato ottenuto coerentemente con il grafico di dispersione. |
|
| |
Soluzione del punto 3. 
|
|
| |
4. Si calcoli il coefficiente di correlazione lineare di Bravais-Pearson e lo si commenti in relazione alle risposte precedenti. |
|
| |
Soluzione del punto 4.
|
|
| |
5. Calcolare la retta di regressione dei minimi quadrati e rappresentarla sul grafico di dispersione. |
|
| |
Soluzione del punto 5.
|
|
| |
6. Calcolare l'indice di determinazione, commentare il risultato ottenuto in relazione alla retta di regressione disegnata e in termini di varianza totale, spiegata e residua. |
|
| |
Soluzione del punto 6.
|
|