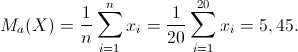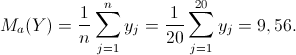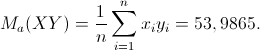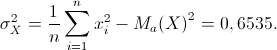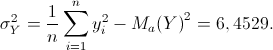ESERCIZIO 3
La seguente tabella riporta in forma di distribuzione unitaria doppia i dati delle regioni italiane relativamente al Quoziente di nuzialità (matrimoni per 1000 abitanti) e al Quoziente di natalità (nati per 1000 abitanti).
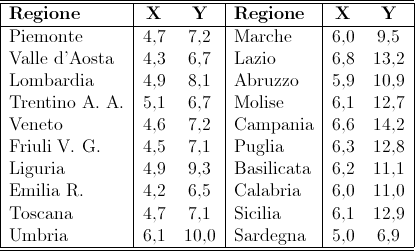
1. Formulare statisticamente la situazione considerata individuando: il collettivo in esame, la sua numerosità, la singola unità statistica, i caratteri considerati e la loro tipologia.
Soluzione del punto 1:
U: Collettivo formato dalle 20 regioni d'Italia; ogni regione rappresenta la singola unità statistica.
La numerosità del collettivo è n=20.
I caratteri considerati sono: X=Quoziente di nuzialità (matrimoni per 1000 abitanti); Y=Quoziente di natalità (nati per 1000 abitanti). I due caratteri sono di tipo quantitativo continuo.
Soluzione del punto 2:
Data la distribuzione unitaria doppia di due caratteri X e Y quantitativi, si definisce baricentro la coppia
data dalle medie aritmetiche dei due caratteri.
Per calcolare le due medie aritmetiche utilizziamo quindi le seguenti formule:
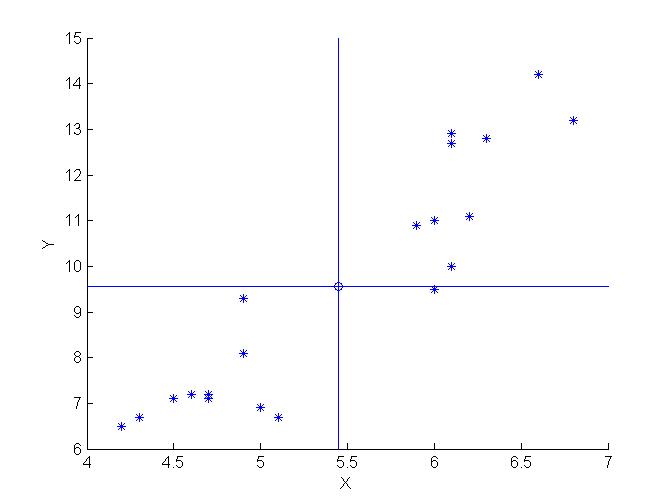
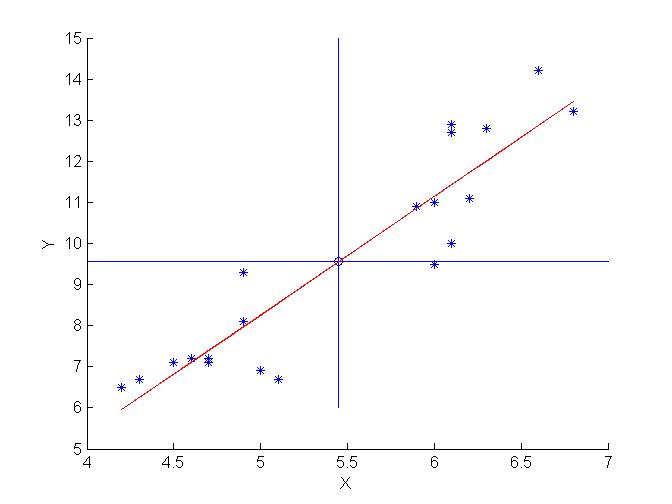
Disegniamo ora il grafico di dispersione:
Soluzione del punto 3:
Avendo già i valori delle due medie aritmetiche dal punto 2., per calcolare la covarianza tra X e Y possiamo usare la formula:
A partire dalla distribuzione unitaria doppia, ricordando che n=20, calcoliamo dunque:
Da cui risulta:
Possiamo quindi concludere che i due caratteri sono positivamente correlati: al crescere dell'uno, anche l'altro cresce. Nello specifico all'aumentare del quoziente di nuzialità, aumenta anche il quoziente di natalità. Scopriremo poi, mediante l'analisi del coefficiente di Bravais-Pearson, in quanta parte tale correlazione è di tipo lineare.Questo risultato conferma ciò che si vedeva anche dal grafico di dispersione, nel quale infatti prevalgono gli scostamenti concordi (I e III quadrante), che fanno sì che la covarianza risulti positiva.
Soluzione del punto 4:
Il coefficiente di correlazione lineare di Bravais e Pearson è definito come:
Calcoliamo quindi la deviazione standard dei due caratteri X e Y ricordando i valori delle due medie aritmetiche ottenute al punto 2. e ricordando che n=20.
Da cui seguono:
In conclusione risulterà:
Anche questo risultato conferma che i due caratteri sono positivamente correlati.
In particolare si ricordi che il coefficiente di correlazione lineare è un indice relativo che assume valori nell'intervallo [-1,1], assumendo il valore degli estremi nel caso di perfetto legame lineare.
Si osservi dunque che in questo caso il coefficiente di Bravais e Pearson indica che la relazione tra i due caratteri considerati si avvicina molto ad una relazione di tipo lineare.
Soluzione del punto 5:
Per calcolare la retta di regressione Y*=a*+b*X bisogna ottenere la coppia (a*, b*) data dalle seguenti formule:
Si noti che il coefficiente di regressione b* è risultato positivo, segno che la retta di regressione avrà pendenza positiva.
Si ottiene quindi la retta di regressione Y*=-6,14+2,88X che si può riportare sul grafico di dispersione:
Si osservi che il valore del coefficiente angolare b*=2,88 ci dice che per ogni aumento unitario del quoziente di nuzialità, il modello prevede un aumento del quoziente di natalità di 2,88.
6. Calcolare l'indice di determinazione, commentare il risultato ottenuto in relazione alla retta di regressione disegnata e in termini di varianza totale, spiegata e residua.