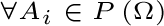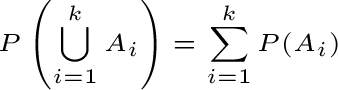|
Agli inizi del XX secolo si sentiva l’esigenza di
sistematizzare in modo rigoroso le diverse concezioni, nel tentativo di
costruire una teoria unificata della probabilità. Emblematico fu che al
congresso di Parigi del 1900 il matematico Hilbert, presentando una lista dei
problemi ancora aperti e di cui urgeva trovare una soluzione, inserisse al
sesto posto l’assiomatizzazione della probabilità. In questo contesto la scelta
degli assiomi da porre a fondamento dell’intera teoria accese un dibattito
molto intenso tra le diverse correnti di pensiero, che rivendicavano la propria
concezione di probabilità come elemento fondante. Nel 1933 viene pubblicata l’opera dello studioso russo A.N. Kolmogorov
“Foundation of the theory of probability” in cui l’autore si poneva volutamente
al di sopra della parti con l’obiettivo di costruire una teoria della
probabilità prescindendo dai diversi significati.
Questa impostazione non dà della probabilità una definizione
diretta ma accetta qualunque approccio, purché questo rispetti le proprietà
fondamentali, assunte come assiomi; da queste si deducono le altre proprietà
come teoremi. Un assioma è un’affermazione che non si dimostra in quanto principio di base universalmente accettato. La teoria assiomatica si fonda su tre momenti fondamentali:
Postulati della probabilitàI) Positività: II) Certezza: III) Unione: P(A∪B) = P(A) + P(B)
NB. Dal primo e secondo assioma si deduce che la probabilità di un evento A è
sempre compresa tra 0 e 1.La teoria assiomatica si fonda su tre momenti fondamentali:
Il terzo postulato si può estendere all'unione di un infinita numerabile di
eventi e tale postulato viene detto postulato della sommabilità completa. A partire da questi tre assiomi, sono stati in seguito formulati veri
teoremi e varie leggi, che costituiscono la base della moderna teoria della
probabilità. Teoremi fondamentali della probabilitàI) Probabilità dell’evento impossibile II) Probabilità dell’evento negazione III) Probabilità totali P(A∪B) = P(A) + P(B) – P(A∩B)
Quest’ultimo teorema generalizza il concetto dell’unione per eventi compatibili. 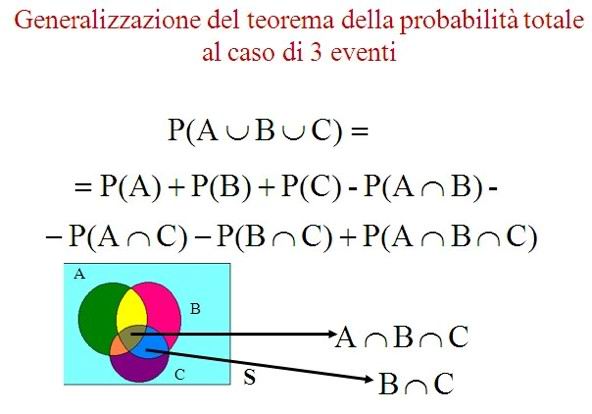
Se per 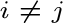 abbiamo abbiamo 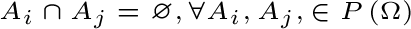 , allora : , allora :
|
pagina precedente
 Torna all'Indice
Torna all'Indice  pagina successiva
pagina successiva