|
A causa delle critiche mosse alla concezione “classica”, agli inizi del ‘900, si assiste ad un grande progresso della concezione “frequentista”, dovuto all’applicazione alle scienze sperimentali. La sistematizzazione e formalizzazione dei risultati è raggiunta da Richard Von Mises (1883-1953). L'esperienza dice che al crescere del numero delle prove fatte tutte nelle stesse condizioni, la frequenza relativa pur variando, tende a stabilizzarsi attorno ad un valore, cioè ordinariamente le fluttuazioni molto grandi sono sempre più rare, e tale valore attorno a cui le frequenze relative si stabilizzeranno corrisponde al valore della probabilità dell'evento. In ciò consiste la legge empirica del caso. Anche se impropriamente potremmo scrivere che 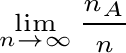 , impropriamente perché non si esclude che si possano avere
scostamenti notevoli dalla probabilità anche per valori alti di , impropriamente perché non si esclude che si possano avere
scostamenti notevoli dalla probabilità anche per valori alti di 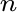 . .Vanno fatte alcune osservazioni: 1. La legge non è dimostrabile ma è puramente empirica 2. Il caso "non ha memoria" per cui se lanciando una moneta viene "testa" molte volte di seguito, ciò non ci autorizza a pensare che nel lancio successivo sia più probabile che esca "croce". Ogni lancio è indipendente dagli altri già effettuati. 3. La legge empirica del caso dà un significato pratico al concetto di probabilità. La probabilità è la frequenza relativa con cui un certo evento tende a presentarsi su un numero grande di prove. 4. La legge empirica del caso legittima la definizione frequentista o statistica di probabilità Si definisce probabilità di un evento in senso statistico la frequenza relativa che esso assume su un grande numero di prove eseguite tutte nelle medesime condizioni Tale definizione si applica in quei casi in cui non è applicabile la definizione classica in quanto viene a mancare la condizione di equiprobabilità degli eventi elementari su cui essa si basa. Ad esempio se abbiamo delle buone ragioni per ritenere che un dado sia truccato, non essendo per esempio costruito con materiale omogeneo, non potremo ritenere equiprobabili l'uscita dei sei numeri per cui non potremo assegnare alla probabilità di uscita del numero 1 il valore 1/6 . L'alternativa è quella di ripetere il lancio del dado un numero elevato di volte, calcolare la frequenza relativa dell'uscita di 1 ed assumere per definizione tale valore come probabilità dell'evento.Il campo di applicazione è molto vasto, si applica a: - fenomeni passati dei quali si posseggano dati statistici che si sono verificati in condizioni analoghe. Per una data popolazione, si può calcolare: - la probabilità di morte o di sopravvivenza o la probabilità di nascita di maschi o di femmine. Si applica nel campo della: medicina, psicologia, economia, meccanica quantistica e in tutte le scienze per le quali si possono utilizzare metodi statistici. La probabilità di un evento è il limite a cui tende la frequenza relativa, al tendere all’infinito del numero delle prove effettuate. P(A)=
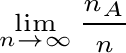 dove dove 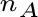 è il numero di
prove nelle quali si è verificato A, è il numero di
prove nelle quali si è verificato A, 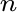 è il numero
totale di ripetizioni della stessa prova. La frequenza relativa di A è data
di è il numero
totale di ripetizioni della stessa prova. La frequenza relativa di A è data
di 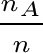 . .
Il
limite viene inteso non nel senso della matematica, ma esprime
semplicemente il fatto che la frequenza relativa
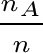 su un gran numero di prove fornisce una "buona" stima della probabilità ( legge empirica del caso) su un gran numero di prove fornisce una "buona" stima della probabilità ( legge empirica del caso)La debolezza di questa definizione è nella sua limitata applicabilità. Per utilizzarla occorre che:
Il grande merito di questa definizione è l'aver stabilito la corretta relazione tra la frequenza e la probabilità, concetti molto diversi, essendo la prima una quantità calcolata a posteriori, cioè dopo aver effettuato l’esperimento, la seconda una quantità, definita a priori. Nella concezione classica la probabilità è stabilita A PRIORI, prima di guardare i dati. Nella concezione frequentista la probabilità è ricavata A POSTERIORI, dall’esame dei dati. Il modello frequentista si può utilizzare solo in esperimenti aleatori che possono essere ripetuti molte volte e sempre nelle stesse condizioni o per quei casi in cui si abbiano a disposizione una notevole massa di dati storici (per esempio si pensi alle tavole di mortalità). Questi esperimenti si incontrano spesso in discipline quali la Fisica, La Biologia, le assicurazioni, la sperimentazione clinica. In una serie di prove, ripetute un gran numero di volte ed eseguite tutte nelle stesse condizioni, la frequenza relativa tende ad assumere valori prossimi alla probabilità dell’evento stesso e l’approssimazione è tanto maggiore quanto più numerose sono le prove eseguite. Esempio: Se negli ultimi 30 anni nella nostra città ha nevicato 18 volte, la probabilità che nevichi in un anno è 18/30=3/5. Esempio: Si vuole calcolare la probabilità che un neonato sia femmina. Su 100.000 nascite si sono avute 48.500 femmine. Essendo il numero di prove sufficientemente elevato ed ogni prova indipendente dall'altra, utilizziamo la definizione frequentista: P(F) = 48500 / 100000 = 0,485 P(M) = 51500 / 100000 = 0,515 Un altro esempio: Qual è la probabilità che un lavoratore abbia un infortunio sul lavoro? Difficile rispondere! Certamente dipende dal lavoro che fa. Un operaio minatore è sicuramente più a rischio di un impiegato alle Poste. Questo perché statisticamente ci sono più infortuni lavorando in una miniera che in un Ufficio Postale. La probabilità frequentista, si misura sulla base di osservazioni statistiche cioè sulla frequenza con cui si registrano determinati fenomeni.
Evento non ripetibile: Probabilità dell’evento: “nel week – end ci sarà il sole” Evento mai realizzatosi: Probabilità dell’evento: “nascerà una zebra senza strisce”
Numero di prove non molto elevato e non ripetibile nelle stesse condizioni: “Probabilità del calciatore di tirare in porta durante lo svolgimento di una partita di calcio” |
pagina precedente
 Torna all'Indice
Torna all'Indice  pagina successiva
pagina successiva