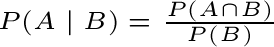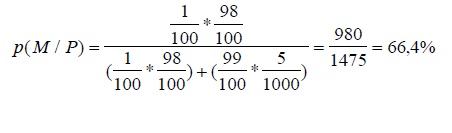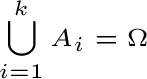|
Studiamo come varia la probabilità, al variare della conoscenza, ovvero al crescere delle informazioni assunte in possesso di chi calcola la probabilità. E' esperienza di tutti i giorni variare il grado di fiducia nelle persone e nelle istituzioni a seconda dei riscontri nella realtà quotidiana. Se a priori pensiamo che molto probabilmente un amico non è bugiardo, la terza volta che scopriamo che ci ha mentito, saremo certamente meno disposti a credergli per il futuro. Il condizionamento è utile quando si vuole analizzare un certo evento A (l’evento condizionato) avendo a disposizione una certa informazione B (l’evento condizionante):
P(A|B) è "la probabilità che si verifica A dato che già si è verificato B"
Si ha quindi che probabilità condizionata di A dato B si ottiene dividendo il numero dei casi favorevoli ad (A∩B) al numero dei casi favorevoli a B, con P(B) ≠ 0. Naturalmente P(B) > 0, se P(B) fosse nullo la probabilità condizionata non avrebbe senso: non è infatti possibile definire la probabilità condizionata rispetto ad un evento impossibile. Non sarebbe inoltre possibile utilizzare la formula indicata in quanto non potremmo dividere per zero. Abbiamo anche detto che il condizionamento degli
eventi si risolve in pratica in una sorta di ridefinizione dello spazio campionario.
Infatti se si assume che B si è verificato ne
consegue che:
1. perdono di rilevanza tutti i punti
campionari che non appartengono a B, cosicché B diviene “una specie” di nuovo evento certo;
2. perdono di rilevanza tutti i punti
campionari di A che non appartengono a B, cosicché l’unica parte di A
che ancora può verificarsi è soltanto A ∩ B.
In pratica, allora, P(A | B) non è altro che P(A ∩ B) riproporzionato sulla base di P(B) che è la probabilità dell’evento condizionante. Nota: Questa operazione non ha alcuna corrispondenza nella teoria degli insiemi. Esempio: 9 studenti: 4 maschi e 5 femmine partecipano ad un concorso. Una delle femmine : Maria ha la probabilità di vincita di 1/9. Prima dell'uscita dei risultati trapela la notizia che la vincitrice è una femmina. La probabilità di vincita di Maria adesso è 1/5 perché nel concorso c'erano 5 femmine. L'informazione extra che la vincitrice è una femmina, ha cambiato la probabilità di vincita di Maria. Se annotiamo con A l'evento "Maria ha vinto" e con B l'evento "una femmina ha vinto", allora la probabilità del evento A condizionato del evento B è P(A|B) è rappresenta la probabilità che l'evento A si verifica dato che B si è verificato. P(A∩B) = P(A) = 1/9, P(B) = 5/9, P(A | B) = (1/9)/(5/9) = 1/5.
Teorema della probabilità composta: P(A ∩ B) = P(A | B) P(B) = P(B | A) P(A). Teorema della probabilità marginale: P(B) = P(B | A)
P(A) + P(B | Ā ) P( Ā )
Questa formula può essere dimostrata, sfruttando le proprietà delle
operazioni fra eventi e della probabilità, attraverso i seguenti
passaggi:
P(B) = P(B ∩ Ω) = P[B ∩ (A ∪ Ā )] = P[(B ∩ A) ∪ (B ∩ Ā )] = P(B ∩ A) + P(B ∩ Ā ) = P(B | A) P(A) + P(B | Ā ) P( Ā ), dove fra le altre cose oltre alla formula di probabilità composte si sfrutta il fatto che (B ∩ A) e (B ∩ Ā ) sono incompatibili (lo si può verificare utilizzando i diagrammi di Venn). Teorema di Bayes (probabilità delle cause): 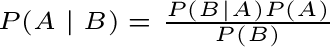 Si
sottolinea che nella pratica il denominatore P(B) è spesso
calcolato a utilizzando la formula della probabilità
marginale e dunque:
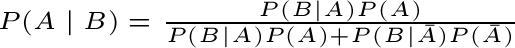 e lega la probabilità a priori P(A) alla probabilità a posteriori P(A|B). Thomas Bayes (1702-1761) ha trovato una formula matematica geniale che fornisce un metodo molto potente di correggere una probabilità alla luce di nuove informazioni. Pertanto, se vi è una stima preliminare di probabilità del verificarsi di un evento e se si hanno nuove informazioni (supplementari), si può ottenere l'esatta probabilità a posteriori della produzione dell'evento. Ripetutamente applicando la formula di Bayes, ogni volta che si hanno nuove informazioni, si possono correggere le probabilità meno affidabili in modo che, finalmente si arrivi alle probabilità probabilmente molto affidabile. Un tipico esempio di applicazione delle formula di Bayes è quello della diagnostica medica: se A è una malattia e B è un sintomo, possiamo ottenere la probabilità che, osservato il sintomo, si abbia la malattia, una volta date P(A) – che può essere ricavata dall’incidenza della malattia nella popolazione in esame, P(B|A), che esprime la probabilità che in pazienti malati si osservi il sintomo – e P(B|non A), la probabilità che il sintomo sussista in assenza della malattia. Osservazione:
Il teorema di Bayes si basa sul concetto di probabilità condizionata e dunque si presupporre che l'esperimento in causa e stato già effettuato almeno una volta. Si offre in questo modo una modalità di correzione della probabilità di un evento in base a informazioni ottenute in seguito a ogni altro esperimento. In questo modo si possono fare delle predizioni che migliorano nella misura in cui l'esperimento viene ripetuto. In base a questa formula si è costruito un intero ramo della statistica matematica denominato "predizione bayesiana". Formalmente il teorema di Bayes è valido in tutte le interpretazioni della probabilità. In ogni caso, l'importanza di questo teorema per la statistica è tale che la divisione tra le due scuole (statistica bayesiana e statistica frequentista) nasce dall'interpretazione che si dà al teorema stesso. Il teorema di Bayes si usa quando un evento B può verificarsi sotto diverse condizioni sulle quali si possono fare n ipotesi. Se si conosce la probabilità delle ipotesi nonché le probabilità condizionate, si potrà verificare se le ipotesi iniziali erano corrette o se devono essere modificate. Esempio: Una malattia colpisce 1 persona su 100.
Un test dà esito positivo nel 98% dei casi su persone effettivamente malate e nello 0,5% dei casi su persone che invece stanno bene. Se una persona fa il test, che probabilità p ha di essere davvero malata se il test dà esito positivo? p(M/P): p che la persona sia malata posto che il test sia positivo
Esempio: In un caso di omicidio ci sono due sospetti, A e B, considerati dalla polizia “ugualmente
sospettati”. Sul luogo del delitto sono stati rinvenuti dei capelli non appartenenti alla
vittima, e quindi appartenenti al colpevole. La prova del DNA sui capelli e sui
due sospetti ha portato alla conclusione che il DNA ritrovato potrebbe
appartenere all’80% ad A e al 50% a B. Qual'è la probabilità che sia A il
colpevole alla luce dell’analisi del test sul DNA? E che sia B?
Sappiamo: P(A) = P(B) = 0,5 P(test|A) = 0,80 e P(test|B) = 0,50 Allora: P(test|A)P(A) + P(test|B)P(B) = 0,8 x 0,5 + 0,5 x 0,5 = 0,65 e P(A|test) = 0,8x0,5/0,65 = 0.6 P(B|test) = 0,5x0,5/0,65 = 0,4 Osservazione: Nel Teorema di Bayes la situazione è “rivoltata”. Si conosce il risultato dell’esperimento e si vuole calcolare la probabilità che sia dovuto ad una certa causa. Alcune delle relazioni precedenti possono essere estese anche a più di 2 eventi: 1. La formula delle probabilità composte può riguardare anche un numero qualsiasi di eventi A1, A2, A3, … Si avrà allora:
P(A1 ∩ A2 ∩ … ∩ Ak) = P(A1) P(A2 | A1) P(A3 | A1 ∩ A2) ... P(Ak | A1 ∩ … ∩ Ak–1) che è detta anche regola della catena.
2. La formula della probabilità marginale
può essere estesa anche ad una partizione dello spazio
campionario Ω più “fine” di quella vista in
precedenza fra A e Ā . Ma vediamo prima cos’è una
partizione.
• incompatibili in quanto non devono avere punti campionari in comune, cioè Ai ∩ Aj = ø per ogni i ≠ j.
Per averne un’idea possiamo immaginare la partizione come le
mattonelle di un pavimento: la loro unione forma il pavimento
(esaustività) ma fra loro non vi sono sovrapposizioni
(incompatibilità).
 Detto cos’è una partizione, la formula della probabilità marginale per una generica partizione A1, A2, ..., Ak di Ω è data da: 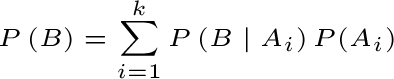 3. Analogamente alla formula della probabilità marginale, anche la formula di Bayes può essere estesa ad una generica partizione A1, A2, ..., Ak di Ω. In tale caso la formula di Bayes è una semplice riscrittura di quella vista in precedenza: 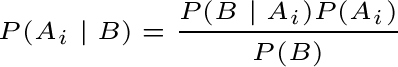 dove normalmente P(B) è ricavato sulla base della formula della probabilità marginale precedente. Precisiamo che da un punto di vista pratico la formula di Bayes assume una rilevanza particolare quando i k eventi Ai possono essere interpretati come possibili “cause” dell'evento B. In tale contesto: P(Ai | B) è detta probabilità a posteriori della causa Ai; P(Ai) è detta probabilità a priori della stessa causa e P(B | Ai) è detta verosimiglianza dell'evento B.
|